Experiment: Proof of the inverse square law
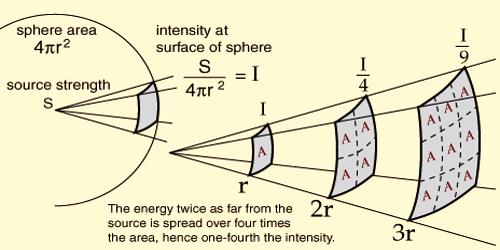
When the sound waves originate from a point source, the emitted wave fronts become spherical. If the distance of observer is very large compared to size of the source, then we can consider the source as point source. Suppose in each second P amount of sound energy is emitted from the source.
Any point source which spreads its influence equally in all directions without a limit to its range will obey the inverse square law. This comes from strictly geometrical considerations. The intensity of the influence at any given radius r is the source strength divided by the area of the sphere. Assume a sphere of radius r around the source. Energy emitted from the source will be equally distributed on the surface of the sphere.
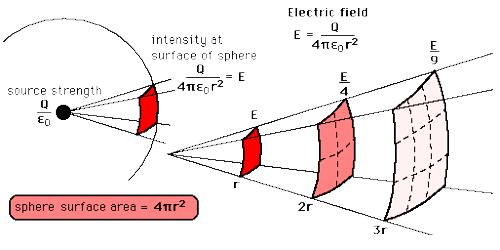
Rate of flow of energy through unit area of the sphere = P/4πr2; here 4πr2 area of the surface of the sphere. According to the definition it represents intensity I, at distance r from the sphere. That means, I = P/4πr2
I = P/4πr2
So, for a fixed source, I ∞ 1/r2, hence inverse square law is verified.