The angular momentum in rotational motion is similar to the linear momentum in translators’ motion. The linear momentum of a particle moving along a straight line is the product of its mass and linear velocity, p = mv.
The angular momentum of a particle is defined as the moment of linear momentum of the particle
Let consider a particle of mass m moving in the XY plane with a velocity v and linear momentum p = m v at a distance r from the origin (Figure).
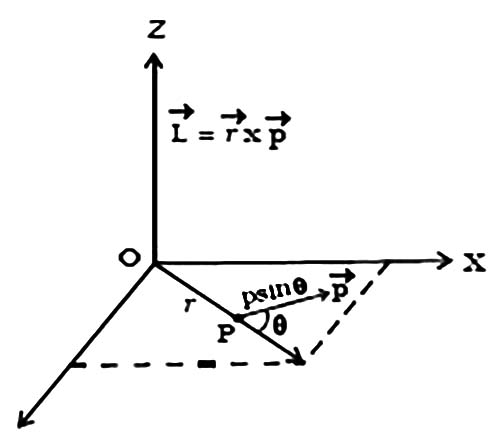
The angular momentum L of the particle about an axis passing through O perpendicular to XY plane is defined as the cross product of r and p.
L = r x p
Its magnitude is given by L = r p sin θ
where θ is the angle between r and p and L is along a direction perpendicular to the plane containing r and p.
The unit of angular momentum is kg m2 s-1 and its dimensional formula is, M L2T-1.