Relation between Internal resistance and Electromotive force of a cell
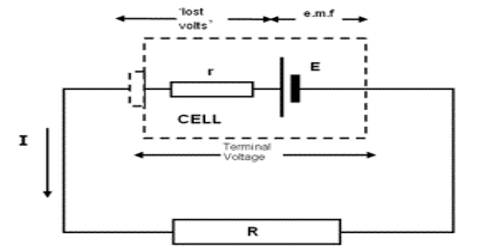
Each energy source, viz, cell or generator, has internal resistance. The amount of resistance which the current experiences inside the cell is called internal resistance of the cell. This resistance is created from the substances by which the cell is constructed. For example, the value of internal resistance in case of a cell depends on the nature of active chemical substances, the distance between the plates of the cell and dimension of those plates, the temperature inside the cell etc. Again, the resistance of the wires used inside the generator, different components etc. is the internal resistance. The internal resistance is connected in series with the resistance of the external circuit [Figure]. So, the total resistance of the circuit.
R = R1 + r, here, R1 is the resistance of the external circuit.
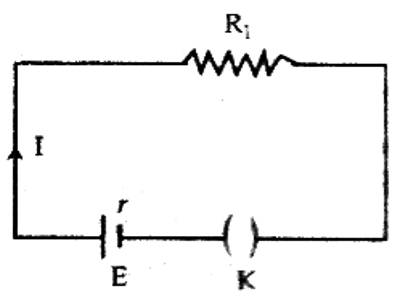
Normally, the value of internal resistance is very low. It the current in the circuit is I, then we get,
I = E / (R1 + r); here E the electromotive force of the cell.
or, E = IR1 + Ir = V + Ir … … (1)
V and Ir are respectively the potential difference between the two ends of the resistance of the external circuit and potential drop for r inside the cell. V is called the terminal potential difference or voltage.
That means V is the potential difference between the terminals of the cell during the flow of current in the circuit.
From equation (1), it is clear that V < E.
The reason for the smaller value of terminal voltage than the electromotive force is due to the fact that some energy is needed for the current to flow through the internal resistance of the cell. As a result, potential drop takes place inside the cell. So it is seen that the potential difference between the two terminals of a cell decreases by an amount of ‘Ir’, that means ‘Ir’ amount of voltage does not contribute in the circuit, rather becomes lost. For this reason, ‘Ir’ is called ‘lost volt‘. According to equation (1), if R1 is very small, the terminal voltage becomes much smaller than the electromotive force. On the other hand, when R1 is very large, then the terminal voltage becomes almost equal to the electromotive force. In equation (1), if 1 = 0, then E = V
i.e., when there is no current in the circuit that means, the circuit remains open, then the potential difference between the two ends at a cell is equal to its electromotive force.