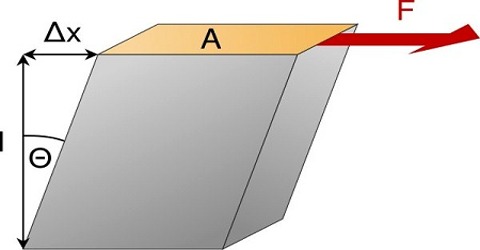
Rigidity modulus
Within the elastic limit, the ratio of the shearing stress and shearing strain is constant. This constant is called rigidity modulus. It is expressed as ‘n’
Rigidity modulus, n = [shearing stress / shearing strain]
Explanation: If a force F applied tangentially on the surface of the body the shearing strain of the surface is θ, an area of the surface is A, then,
n = [(F/A); or, n = F / Aθ.
Unit and dimension of rigidity modulus are identical to those of Young’s modulus. The modulus of rigidity is denoted by G and expressed in pascals. Modulus of rigidity value of a material is determined by a torsion test.

Modulus of Rigidity can be determined by performing a tensile stress test where stress vs strain is plotted. The slope of the line is equal to the Modulus of Rigidity. Rigidity modulus of iron is 7.7 x 1010 Nm-2 means that in order to produce one-radian angular rotation the upper surface of the cube of iron the force needed to apply on the upper surface of the cube is: 7.7 x 1010 N.