Dependence of Terminal Velocity
(a) Terminal velocity at a point is inversely proportional to the coefficient of viscosity.
(b) Terminal velocity is directly proportional to the difference of densities of the body and the liquid.
(c) Terminal velocity is directly proportional to the square of radius of the falling sphere.
Try to understand the following example.
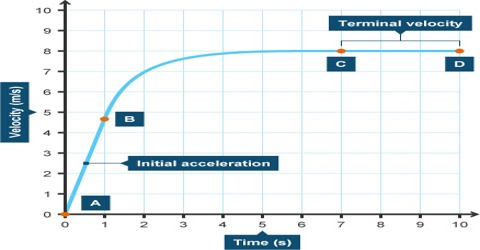
From the above points we can definitely understand that the velocity of a falling body will increasingly reach to a high value for the acceleration due to gravity, but in practice that does not happen. Why?
When a drop of rain falls through atmosphere its velocity continues to increase due to gravitation and due to viscosity retarding or opposing force of atmosphere also increases. At one time resultant acceleration becomes zero. Then the drop continues to fall at constant velocity. This velocity is the terminal velocity. So, due to acquiring terminal velocity the drop of rain does not attain very high velocity.
Consider a falling body. It is acted on by gravity and a drag force due to the air. When the body begins to fall the speed is slow and thus its drag force is also small. The acceleration of the falling body is g. As the body’s speed increases so too does the drag and at some point the speed would increase to the point where the drag force would act to cancel out the force due to gravity. Thus the body no longer accelerates and the speed remains constant.