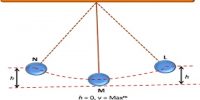
A liquid in motion possesses pressure energy, kinetic energy and potential energy.
Pressure energy:
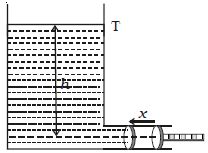
Consider a liquid of density p contained in a wide tank T having a side tube near the bottom of the tank as shown in Figure. A friction less piston of cross sectional area ‘a’ is fitted to the side tube. Pressure exerted by the liquid on the piston is P = h ρ g.
Where h is the height of liquid column above the axis of the side tube. If x is the distance through which the piston is pushed inwards, then
Volume of liquid pushed into the tank = ax
Mass of the liquid pushed into the tank = axρ
As the tank is wide enough and a very small amount of liquid is pushed inside the tank, the height h and hence the pressure P may be considered as constant.
Work done in pushing the piston through the distance x = Force on the piston x distance moved
(i.e) W = Pax
This work done is the pressure energy of the liquid of mass axρ.
Pressure energy per unit mass of the liquid = Pax/asρ = P/ρ