Electric field due to two charged parallel sheets:
Consider a thin plane infinite sheet having positive charge density σ. In order to find the electric field intensity at a point p, which is at a perpendicular distance r from the plane shell, we choose a closed cylinder of length 2r, whose ends have an area as the Gaussian surface.
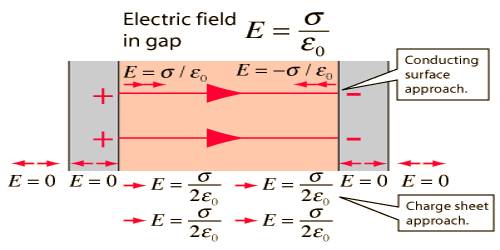
Let M and N be two parallel charged conductors [Figure]. The sheet M is positively charged and the sheet N is negatively charged and are charged with the same density. The charge density of both of them is σ. Electric field E→ at a point between the two sheets is to be found out.
Now, the magnitude of the electric field at point P due to the sheet M will be E1 = σ / 2ε0; and its direction will be along MN. Again for the sheet N magnitude of the electric field at point P will be E2 = σ / 2ε0; and since the sheet N is charged negatively, so the direction of E2 will be along MN.
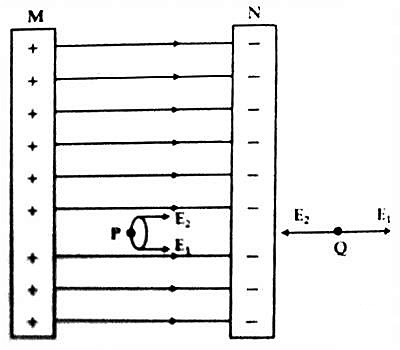
Hence magnitude of the total electric field at point P will be,
E = E1 + E2
= (σ / 2ε0) + (σ / 2ε0)
So, E = σ / ε0 … … (1)
The direction of the electric field will be from sheet M to N i.e., from positive charge to negative charge.
At a point Q outside the two sheets, the magnitude of the electric field due to the sheets M and N will be E1 = σ / 2ε0 and E2 = σ / 2ε0 respectively. But as they act opposite to each other so the net field will be zero. That means, there will not be electric field outside the two sheets.
In Conclusion, E due to two oppositely charged infinite plates is σ/ε0 at any point between the plates and is zero for all external points.