Work done by a Constant Force
The work done by a constant force is proportional to the force applied times the displacement of the object. A force does not have to, and rarely does, act on an object parallel to the direction of motion.
A body can be raised above or lowered down by small amount in the sphere of gravitational force. Since the height is small, so we can consider gravitational force constant. (F = mg, as g is constant, so F is constant.)
That means, if the magnitude and direction of the force is not changed, then that force is called constant force.
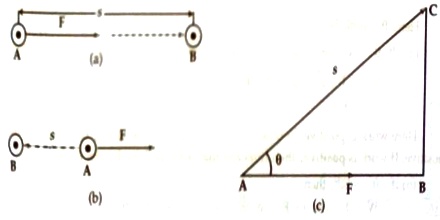
Let a force F be applied at point A of a body along AB and due to this the body moving from point A to point B coven a distances [fig-a]. Then,
Work done = magnitude of the force x magnitude of displacement along the point of action of the force
or, W = F x s
If due to the application of force the displacement of the body i.e., the point of actions of the force to apposite to the direction of force i.e., AB = s [Fig-b], then,
Work done = magnitude of the force x magnitude of displacement along the direction of the force.
or, W = F x (-s) = – F x s
Negative sign is used to indicate that force and displacement are opposite to each other.
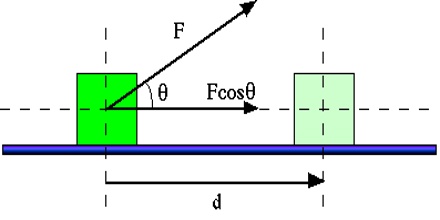
Now, consider that due to the action of force F on a body along direction AB, the body reaches to point C covering a distance s making an angle θ with the direction of the applied force [Fig- c]. Then displacement of the body along the line of action of the force = AB = s cos θ.
Here, BC ┴ AB
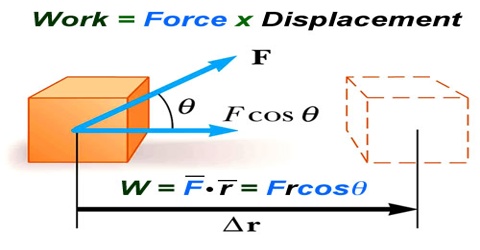
Work done, W = magnitude of force x magnitude of displacement along the direction of force
or, W = Fs cos θ
= magnitude of force x component of displacement along the line of action of the force
= magnitude of displacement x component of force along the direction of force.
Work can be expressed by vector algebra as:
Work is measured by the scalar product of two vectors, force and displacement.
Suppose, force F is a vector quantity and displacement ‘s’ is also a vector quantity.
So, work = force x displacement
or, W = F. s
= s . F = Fs cos θ,
[s cos θ is the component of displacement along the direction of force, F]
Here, θ = angle between F and s.