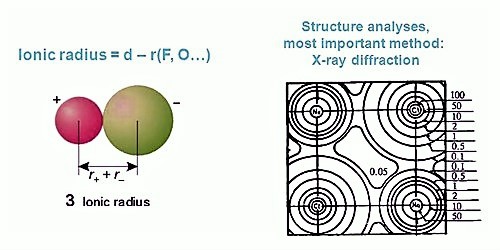
The radius of an isolated ion is complicated to define. Theoretically, the radius of an ion extends to infinity. So the absolute radius of an ion is not doable to determine. The radius is evaluated from the experimental space between two nearest neighbors.
Pauling has calculated the radii of the ions on the basis of the observed internuclear distances in four crystals namely NaF, KCl, RbBr, and CsI; this calculation named Pauling’s Method. In each ionic crystal, the cations and anions are isoelectronic with inert gas configuration.

Further the following two assumptions are made to assign the ionic radii.
(i) The cations and anions of an ionic crystal are assumed to be in contact with each other and hence the sum of their radii will be equal to the inter nuclear distance between them.
r(C+) + r(A–) = d (C+ – A–) … … … … (1)
where,
r(C+) – radius of cation, C+
r(A–) – radius of anion, A–
d(C+ – A–) – internuclear distance between C+ and A– ions in C+ A– ionic crystal
(ii) For a given noble gas configuration, the radius of an ion is inversely proportional to its effective nuclear charge. i.e.
r(C+) α 1/ Z*(C+) … … … (2)
r(A+) α 1/ Z*(A–) … … … (3)
where, Z*(C+) & Z*(A–) are the effective nuclear charges of cation (C+) and anion (A–) respectively. On combining (2) & (3)
r(C+)/ r(A+) = Z*(A–)/ Z*(C+) … … … … (4)
Hence the above two equations (1) & (4) can be used to evaluate the values of r(C+) and r(A–) provided that the values of d(C+ –A–), Z*(C+) and Z*(A–) are known.
When a neutral atom gains an electron to become an anion (-ve ion), its radius increases. This is projected due to the increase in the number of electrons which the similar nuclear charge has to hold. The force of attraction on the electrons decreases and so the radius increases.
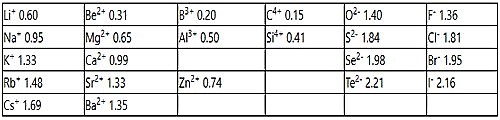
Table: Pauling set of ionic radii
Linus Pauling was the original scientist to explain the phenomena of electronegativity. The best method to explain his method is to look at an imaginary molecule that we will call XY. By comparing the considered X-Y bond energy with the theoretical X-Y bond energy (computed as the average of the X-X bond energy and the Y-Y bond energy), we can explain the comparative affinities of these two atoms with deference to each other.
Δ Bond Energies = (X-Y)measured – (X-Y)expected
If the electronegativities of X and y are similar, then we would imagine the calculated bond energy to equal the theoretical (expected) bond energy and consequently, the Δ bond energies would be zero. If the electronegativities of these atoms are not similar, we would see a polar molecule where one atom would start to pull electron density toward itself, causing it to become moderately negative.
The number of positive charges in the nucleus resolves both the number of electrons that enclose an atom and the number of electrons that can be misplaced or gained to form ions. Thus as the charge on the ion becomes more positive, there will be fewer electrons and the ion will have a lesser radius.
As the charge on the ion becomes more negative, there will be more electrons and the ion will have a bigger radius. As the atomic figure increases in any given feature of the Periodic Table, the number of protons and electrons increases and thus the size of the atom or ion increases.