Gaseous Equilibria
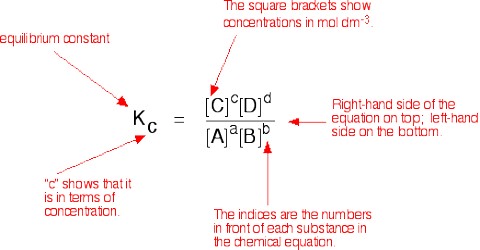
The concentrations of gases in a mixture usually are expressed in terms of the partial pressure of the gases. Since the partial pressure of an ideal gas is proportional to its concentration, c, the expression for the equilibrium constant for the reaction,
a A (g) + b B (g) ↔ l L(g) + m M (g) may be written in the form
KP = [PlL x PmM] / [PaA x PbB]
when KP, is the equilibrium constant in terms of partial pressure and the partial pressures are the equilibrium values KP and KC are not always identical. This is because the partial pressures are proportional to, but not equal to, gas concentration expressed in mol L-1.
Example: The gases SO2, O2 and SO3 were allowed to come to equilibrium in a closed vessel under certain conditions of temperature and pressure. The partial pressures of the gases were PSO2 = 0.050 atm, PO2 = 0.025 atm and PSO3 = 1.00 atm. Find the values of KP, for the following equilibria:
(a) SO2 (g) + ½ O2 (g) ↔ SO3 (g)
(b) 2 SO2 (g) + O2 (g) ↔ 2 SO3 (g)
Solution: For, (a); KP = PSO3 / (PSO2 + PO2) = 1.00 / (0.050 x 0.0251/2) = 126.58
For, (b); KP = P2SO3 / (P2SO2 + PO2) = 1.002 / (0.0502 x 0.025) = 16×103
It can be seen that the value of a equilibrium constant for the same reaction may be different when the mole ratios of the reactants and products are shown differently in balanced equation.