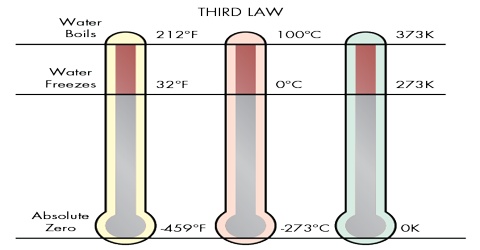
Properties of Third Law of Thermodynamics
The kinetic molecular theory of matter emphasizes the fact that the microscopic or bulk property of matter is a consequence of the motions and positions of the constituent atoms or molecules. There may be a large number of arrangements in respect of position and velocity of the molecules which will give the required macroscopic property. Each arrangement which gives the same bulk property is known as a microscopic state. The microscopic state of a system changes very rapidly as the molecules are always in motion and, in the gaseous state, are colliding with each other with a high frequency. Since the time of a collision is small, even during the time it takes to measure a macroscopic property of a gas, such as pressure, the microscopic state of the system must change a large number of times. In spite of this rapid change of the microscopic state the bulk properties of a system at equilibrium are constant. The number of microscopic states associated with a particular macroscopic state is defined as thermodynamic probability, W, of that state.

This number also represents the number of different ways in which the given state of the system can be realized. It is assumed that all microscopic states are equally probable. At equilibrium the thermodynamic probability is maximum. Since entropy of a system at equilibrium is maximum, it was thought reasonable to relate thermodynamic probability with entropy by the relation,
S = k ln W
where k is the Boltzmann constant. That the relationship between S and W is logarithmic may be shown by considering two systems with entropies S1 and S2 and thermodynamic probabilities W1 and W2 respectively. It the systems are combined the probability of the resulting system will be W1 x W2 but the entropy will be S1 + S2. A relation of the type shown in equation (1) will satisfy this condition. It must be understood, however, that this is not a complete proof of the relation between S and W. Equation (1) is the basis of statistical thermodynamics and leads to calculation of absolute entropies from molecular constants such as mass, moment of inertia, frequency of vibration of bonds. Such calculations are independent of the third law of thermodynamics.