Consider a liquid to flow steadily through a pipe as shown in the Figure. The layers of the liquid which are in contact with the walls of the pipe have zero velocity. As we move towards the axis, the velocity of the liquid layer increases and the centre layer has the maximum velocity v. Consider any two layers P and Q separated by a distance dx. Let dv be the difference in velocity between the two layers.
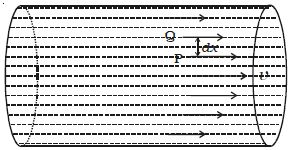
The viscous force F acting tangentially between the two layers of the liquid is proportional to
(i) area A of the layers in contact
(ii) velocity gradient dv/dx perpendicular to the flow of liquid.
So, F α A (dv/dx)
Or, F = η A (dv/dx)
where η is the coefficient of viscosity of the liquid.
This is known as Newton’s law of viscous flow in fluids.
If A = 1m2 and dv/dx = 1s-1
then F = η
The coefficient of viscosity of a liquid is numerically equal to the viscous force acting tangentially between two layers of liquid having unit area of contact and unit velocity gradient normal to the direction of flow of liquid.
The unit of η is N s m-2. Its dimensional formula is ML-1T-1.