(i) Impulsive Force
An impulsive force is a very great force acting for a very short time on a body, so that the change in the position of the body during the time the force acts on it may be neglected. It is defined as the rate of change of momentum in a reaction. It is measured by the transform of momentum in the body it acts on.
This force is much stronger than any other force accessible at that point of time and acts on an object for a very little time during collision or explosion
Real-life Example:
- The blow of a hammer, the collision of two billiard balls, etc.
- The long jump pit is filled with sand to increase the reaction time when athlete land on it.
- When a batsman plays a shot for six, a force acts on a ball through a bat for a short interval of time. We call that force, an impulsive force.
Mathematical Example:
A car of mass 1000kg is traveling with a velocity of 25 m/s. The car hits a street lamp and is stopped in 0.05 seconds. What is the impulsive force acting on the car during the crash?
Answer:
m = 1000kg, u = 24 m/s, v = 0, t = 0.05s, F = (mv−mu)t
Then, F = [(1000)(0)] – [(1000)(24)] / 0.05F = 480,000 N.
(ii) Impulse of a force
Impulse of a force is the force multiplied by the duration of time for which it acts. In other words, it is the transform of momentum the force causes in anybody.
The impulse J of a constant force F acting for a time t is defined as the product of the force and time.
Impulse = Force x time
Or, J = F x t
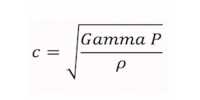
The impulse of force F acting over a time interval t is defined by the integral.
J = t∫oF dt
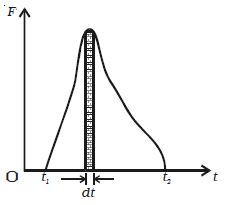
The impulse of a force therefore can be visualized as the area under the force versus time graph as shown in Figure. When a variable force acting for a short interval of time, then the impulse can be measured as,
J = Faverage x dt
The impulse of force is a vector quantity and its units are N s.
Another way,
Thus, Impulse = Force * Time
From Newton’s Second Law of Motion
F = ma, where F is a force, ‘m’ is mass and ‘a’ is an acceleration
but acceleration = change in velocity/time i.e. a = (v-u)/t, where v is the final velocity and u is the initial velocity
implies, F= m(v-u)/t
implies, F*t = m(v-u)
implies, F*t = mv – mu [mv: final momentum, mu: initial momentum]
i.e. Impulse = change in momentum
So, the impulse can also be considered as the change in momentum of an object.
Now, it is proved that, Impulse of force is the product of the average force and the time in which the force acts.