Simple harmonic motion is a motion where a restoring force is functional that is comparative to the displacement and in the reverse direction of that displacement
A particle is said to execute simple harmonic motion if its acceleration is directly proportional to the displacement from a fixed point and is always directed towards that point.
Consider a particle P executing SUM along a straight line between A and B about the mean position O (Figure). The acceleration of the particle is always directed towards a fixed point on the line and its magnitude is proportional to the displacement of the particle from this point.
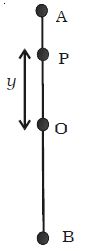
a ∞ y
By definition a = – ω2 y
Where, ω is a constant known as angular frequency of the simple harmonic motion. The negative sign indicates that the acceleration is opposite to the direction of displacement. If m is the mass of the particle, restoring force that tends to bring back the particle to the mean position is given by
F = – m ω2 y
Or, F = – k y
The constant k = m ω2, is called force constant or spring constant. Its unit is N m-1. The restoring force is directed towards the mean position. Thus, simple harmonic motion is defined as oscillatory motion about a fixed point in which the restoring force is always proportional to the displacement and directed always towards that fixed point.