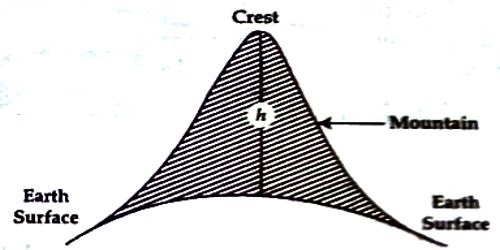
Determination of height of a mountain by simple pendulum
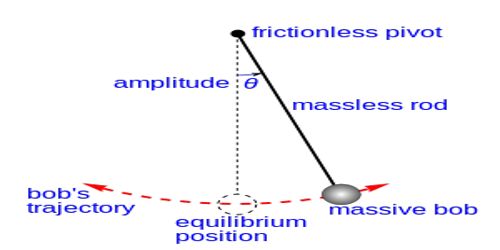
We can determine the height of a mountain or a tall building from earth’s surface by a simple pendulum [Figure]. For this, we need to measure the time periods of oscillation at the bottom and at the top of the mountain. Let the two time periods be T and T1 and if g and g1 be the values of the acceleration due to gravity at the bottom and at the top of the mountain respectively, then,
T1/T = √(g/g1)
Nov from Newton’s law of gravitation, at the bottom of the mountain,
g = GM/R2 … … (1)
and at the top of the mountain,
g1 = GM/(R+h)2 … … (2)
Here, M = mass of the earth, R = radius of the earth and h = height of the Mountain.
Dividing equation (1) by equation (2) we get,
g/g1 = (R + h)2 / R2 = (H x h/R)2
or, (R + h) / R = √(g/g1) = T1/T
or, 1 + h/R = T1/T
or, h/R = T1/T – 1
or, h = R (T1/T – 1) … … … (3)
In equation, (3), T, T and T1 is known, so h can be find out.