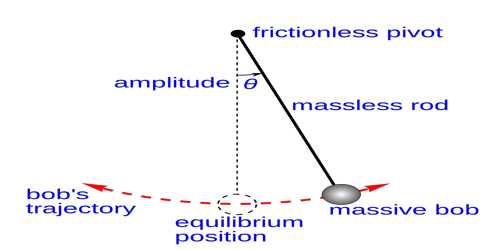
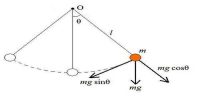
Second Law of Simple Pendulum —Law of length: When the angular amplitude of oscillation does not exceed 4°, the time period of a simple pendulum at a particular place is directly proportional to the square root of its effective length.
If T is the time period and L is the effective length of a pendulum, then according to law T ∞ √L, provided θ ≤ 40 i.e., if effective length is increased 4 times the time period will increase two times or if effective length decreases four times the time period will decrease two times.
If the time period for effective lengths L1 and L2 are respectively T1 and T2, then-
T12/L1 = T22/L2.
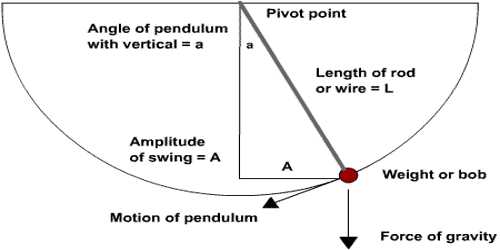
Explanation
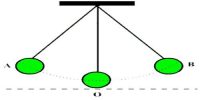
The second law of the simple pendulum states that the period of oscillation of a simple pendulum of constant length is independent of the size, shape, mass and material of the bob, provided it is not very light, such as cork. Let us verify the second law of the simple pendulum. Take three bobs of different masses and different materials. Set up a simple pendulum with the first bob for a fixed length, say 50 cm. Choose amplitude, say 5 cm and pull the bob to a side. Now release the bob and make it to oscillate. Start the stop watch when the bob is at one of its extreme positions. Count 20 oscillations and stop the stop watch. Note the time taken for 20 oscillations. Calculate the time taken for one oscillation, which gives the time period of simple pendulum. Tabulate the readings. Now repeat the procedure with the second bob and the third bob by keeping the length of the pendulum and the amplitude the same. Then tabulate the readings. It will be observed that the period of oscillation does not change with the mass and material of the bob, provided the length of the pendulum and amplitude are constant. This verifies the second law.