Fourth Law—Law of Mass:
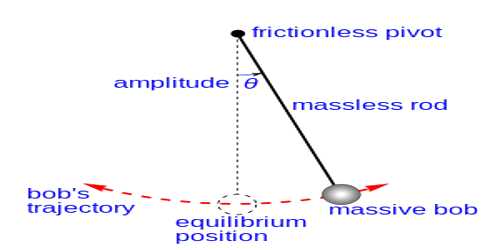
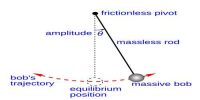
When the angular amplitude does not exceed 4°, time period of a simple pendulum of given length at a particular place is independent of the mass or material of the bob. That is, whether the bob is large or small, hollow or solid or made of copper or silver, the time period T at a particular place will remain constant, provided the effective length remains constant.
“Deduction of the equation of time period from the laws of simple pendulum”
From second and third laws of simple pendulum we get,
T ∞ √L, when θ ≤ 40 and
T ∞ 1/√g, when θ ≤ 40 and L is constant.
Combining these two laws, we get,
T ∞ √(L/g), when both L and g vary and θ ≤ 40
or, T = k √(L/g), where k is a constant, whose value is taken to be 2π.
If the value of g at a place is known and determining the value of L and T by experiment and then value of k is found out from the abuse equation which becomes equal to 2π.
By putting the value of k in the above equation we get,
T = 2π √(L/g) … … … (1)
Based on the laws of the simple pendulum and experimental results, the time period of a simple pendulum is given as: T = 2 π √(L/g)
From equation (1), we can write the relation between the time period of a pendulum and acceleration due to gravity as T is inversely proportional to √g. This relation is referred to as the fourth law of the simple pendulum.
This is the equation of the time period of a simple pendulum. The value of g can be determined from the equation (1) by knowing L and T.