Entropy change in an irreversible process
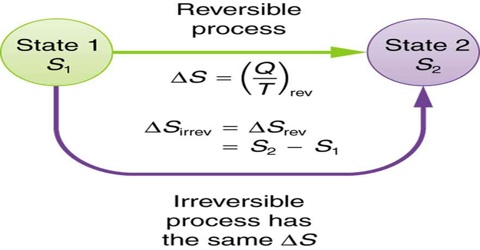
Entropy is a state function and ∆S, in going from an initial state A to a final state B, is always the same and is independent of the path followed. It makes no difference whether the path is reversible or irreversible. For a reversible path, the entropy change is given by,
∆S = SB – SA = B∫A (qrev/T) … … … (1)
If the transfer from state A to state B is carried out irreversibly even then the entropy change is given by equation (1). The entropy change in an irreversible process may, therefore, be calculated if one can determine the amount of heat that would be absorbed, if the process were carried out reversibly. For example, a mole of gas at 5 atm pressure and at 25°C may be expanded to a larger volume at 1 atm and at the same temperature by reducing the pressure in a single step. This would be an irreversible process because at no stage of the expansion process equilibrium was maintained. The heat absorbed during this process could not be used for calculating the entropy change. In order to obtain the entropy change for this expansion process, one has to carry out the process in a reversible manner and determine the heat absorbed when the process is so conducted.
We know that in a reversible process the work done is maximum (Wmax); and in going from state A to state B the change in internal energy, ∆U, of the system is the same whether the change is carried out reversibly or irreversibly. From the first law of thermodynamics, we know that the heat absorbed in the irreversible path is less than the heat absorbed when the path is reversible. Consequently,
dqirry/T < dqrev/T
Also in an irreversible cyclic process, the sum of the dq/T terms is always less than zero;
∫ dqrev/T < 0
This can also be shown from a consideration of the efficiency of cyclic processes. In the reversible cycle, the efficiency is maximum. The efficiency of an irreversible cycle must then be less than that of a reversible cycle operating between the same temperatures of the source and the sink. It follows, then, that for an irreversible process,
[(q2 – q1) / q2] < [(T2 – T1) / T2]
and therefore,
[(q2/ T2) + (q1/ T1)]
For the inequality to hold it is not necessary for both the stages to be irreversible; the relation is valid even if any one of the stages is irreversible. In general, for any cyclic process, if one or more of the steps of the cycle is in-eversible, the sum of the q/T terms will be less than zero.