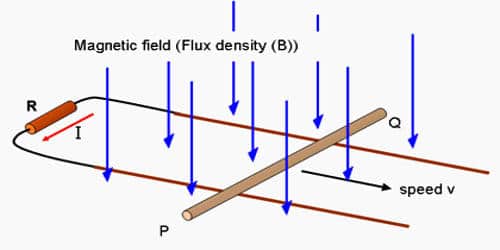
Minimum things required to induce emf are conductor, flux, and movement of the conductor in the magnetic field. EMF induced by changing the area enclosed by the coil. Self-induced emf is the e.m.f induced in the coil due to the change of flux produced by linking it with its own turns. Electric current can be induced in a coil due to the relative motion between the coil and a magnetic field.
Emf induced by changing the area enclosed by the coil
Let consider, PQRS is a conductor bent in the shape as shown in the Figure. L1M1 is a sliding conductor of length l resting on the arms PQ and RS.
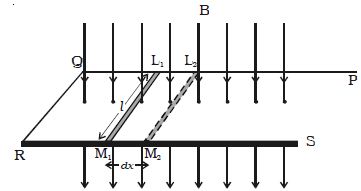
Fig: Emf induced by changing the area
A uniform magnetic field ‘B’ acts perpendicular to the plane of the conductor. The closed area of the conductor is L1QRM1. When L1M1 is moved through a distance dx in time dt, the new area is L2QRM2. Due to the change in area L2L1M1M2, there is a change in the flux linked with the conductor. Therefore, induced emf is produced.
Change in area dA = Area L2L1M1M2
∴ dA = l dx
Change in the magnetic flux, dφ = B.dA = Bl dx
But e = – dφ/dt
∴ e = – Bl dx/dt = – Bl v
where v is the velocity with which the sliding conductor is moved.
Suppose there is a magnet flux produced by permanent magnets of flux density B tesla, a conductor of length l m and conductor is moving in a magnetic field with velocity v m/s in a direction θ° angle from the direct line of the magnetic field. EMF induced (e) in the conductor is given by:
e = B l v Sinθ Volts
From this equation, it can be seen that induced emf depends upon flux density, the effective length of the conductor, the velocity of the conductor, and the angle between velocity direction and flux direction. So, in short, induced EMF depends on a number of turns of the coil, dimensions of the coil, type of the winding, core material of the coil, core dimensions of the coil and the flux density of the external time and/or position varying magnetic field which is causing the induced emf. Faraday’s law can be written: The negative sign in Faraday’s law comes from the fact that the emf induced in the coil acts to oppose any change in the magnetic flux.