Explain Surface Temperature of the Sun

The Sun is a perfect black body of radius r and surface temperature T. According to Stefan’s law, the energy radiated by the Sun per second per unit area is equal to σT⁴.

Where σ is Stefan’s Constant. Hence, the total energy radiated per second by the Sun will be given by:

E = Surface area of the sun X σT⁴

so, E = 4πr² X σT⁴ … …. (1)

Let imagine a sphere with Sun at the centre and the distance between the Sun and Earth R as the radius (Fig). The heat energy from the Sun will necessarily pass through this surface of the sphere.

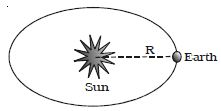
If S is the solar constant, the amount of heat energy that falls on this sphere per unit time is

E = 4πr² S … … … (2)

By definition, equations (1) & (2) are equal.

so, 4πr² σT⁴ = 4πr² S

then, T⁴ = R²S/σr²

so, T = [R²S/σr²]^1/4

or, T = (R/r)^1/2 (S/σ)^1/4

Knowing the value of R, r, S and σ the surface temperature of the Sun can be calculated.