Consider a mass (m) attached to an end of a spiral spring (which obeys Hooke’s law) whose other end is fixed to a support as shown in Figure. The body is placed on a smooth horizontal surface. Let the body be displaced through a distance x towards right and released. It will oscillate about its mean position. The restoring force acts in the opposite direction and is proportional to the displacement.
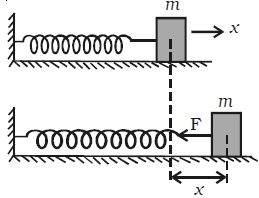
Restoring force F = – kx.
From Newton’s second law, we know that F = ma
So, ma = – kx
So, a = (-k/m)*x
Comparing with the equation of simple harmonic motion, a = – ω2x
We get, ω2 = (k/m)
Or, ω = √( k/m)
But, T = 2π/ω
Time period = T = 2π √( m/k)
And frequency, n = 1/T = 1/2π [√( k/m)]