Kirchoff’s Laws
The concept of the laws Current and resistance in a simple circuit can be determined by using Ohm’s law. But if the circuit is complex then Ohm’s law is not sufficient. For this reason, Kirchhoff’s two laws are used to calculate current and resistance in a complex circuit. Kirchhoff’s Laws for current and voltage lie at the heart of circuit analysis. With these two laws, plus the equations for individual component (resistor, capacitor, inductor), we have the basic toolset we need to start analyzing circuits. Of course, these laws can also be used in simple circuits. Kirchhoff’s laws can be expressed in the following ways.
There are two Kirchhoff laws, the voltage law, and the current law. These two laws can be used to determine all voltages and currents of circuits.
- Kirchhoff’s voltage law (KVL) states that the algebraic sum of the voltage rises and voltage drops around a loop must be zero.
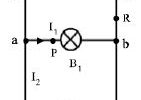
- Kirchhoff’s current law (KCL) states that the algebraic sum of all the currents entering and leaving any node in a circuit is zero.
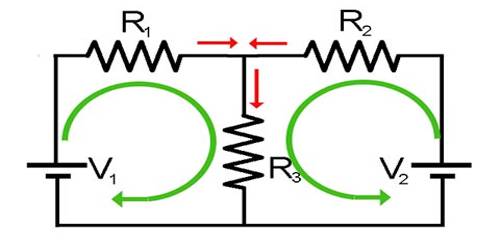
First law: In any electrical network, the algebraic sum of currents meeting at a junction is always zero. This law is known as the current law.
Second law: The total emf within a closed circuit is equal to the algebraic sum of the products of currents and resistances in different branches of that circuit.
The first law is a simple statement of the meaning of potential. The second law is the statement of current conservation.