Transmission lines are electrical cables which consist of two parallel conductors of uniform cross section, usually separated by a dielectric, and which are designed to transmit radio frequency ( ≈ KHz to ≈ 300 MHz) signals from one place to another. Examples include twin lead (two parallel wires), coaxial cable and the strip line. At lower frequencies (50 Hz or 60 Hz) overhead power lines are used to transmit electricity from a remote generating station to a city. At microwave frequencies 300 MHz to 300 GHz) waveguides are used, for infrared frequencies specialised waveguides are made of layers of different dielectrics, and at optical frequencies we see the application of optical fibres. In this section we shall only discuss transmission lines which comprise two parallel conductors.
We will consider a section of a transmission line as if it were an electrical circuit, and so we need to briefly review the circuit rules due to German physicist Gustav Kirchhoff (1824-1887). His first rule, the junction rule, expresses conservation of charge – it requires that the rate at which charge flows into a junction must equal the rate at which charge flows out of that junction. This is conveniently expressed in terms of currents as: “at any point, the sum of all currents entering a junction must equal the sum of all currents leaving that junction”. For the junction shown in below Figure (a) this implies I2 + I3 + I4 = I1
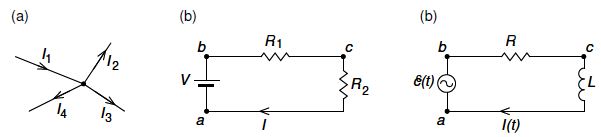
Circuits to illustrate (a) Kirchhoff’s junction rule, and (b) Kirchhoff’s loop rule.
Kirchhoff’s 2st rule, the loop rule, expresses energy conservation, and requires for DC circuits that the sum of the changes in potential around any closed path of a circuit must be zero. For the circuit shown in Fig (b) which, from Ohm’s law, has current I = V/(R1 + R2) flowing around it this implies
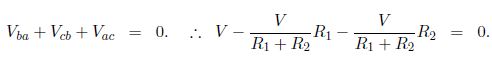
In AC circuits which include inductors, the electric field is not conservative and so the potential is undefined. However, we can still use Kirchhoff’s 2nd rule if for the change across an inductor we use the emf. Hence, for the AC circuit in Fig (c) we have
Ɛ (t) – I (t) R – L (dI/dt) = 0.