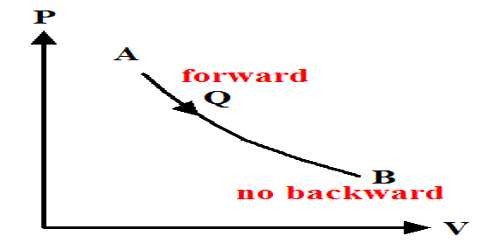
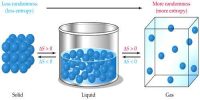
The thermal property that remains constant in the adiabatic process is called entropy. It is stored as potential energy in a form that can do adequate work to reinstate the system plus surroundings to their primary conditions. Alternately, entropy is the physical property of the body that remains constant in an adiabatic process. The entropy is merely transferred from the system to the surroundings.
Actually in all adiabatic compression process entropy does not remain constant. Entropy always accompanies heat transfer. But there are also other sources of entropy such as friction which is commonly called irreversibilities. Hence for only reversible adiabatic procedure entropy remains constant also known as an isentropic procedure.
The entropy of reversible process: We know that the freezing of water at the meting point is a reversible process.
Calculation of entropy for the system (the water) and surrounding for this freezing process is simply heat divided by melting temperature. The total entropy change of this process is thus zero, demonstrating the statement of the second law of thermodynamics.
The most common example is an isothermal reversible expansion of an ideal gas, as in the first step of a Carnot cycle. From Carnot’s cycle, it is seen that AB and CD are two isothermal expansion and compression lines. On the other hand, since BC and DA are two adiabatic expansion and compression lines so no change of heat occurs. Change of entropy along the isothermal line. Mathematically, at every point of a P-V diagram, the system is at equilibrium such that the external pressure equals the internal pressure.
AB = Q1/T1
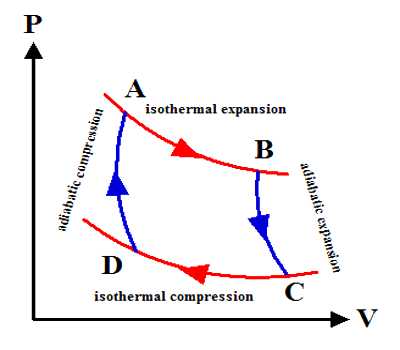
Mathematically, there is never any dissimilarity in pressure. We move from point to point on a curve without thinking of it as a physical expansion that requires a pressure dissimilarity.
Change of entropy along the isothermal line:
CD = Q2/T2
A total change of entropy of the working substance = Q1/T1 = Q2/T2
But Carnot’s cycle = Q1/T1 = Q2/T2
So, Total change of entropy, dS = (Q1/T1) – (Q2/T2) = 0
So, entropy remains constant in the reversible cycle.
Mathematical Example:
One kg of superheated steam at 0.2MPa and 2000C contained in a piston-cylinder assembly is kept at ambient conditions of 300K till the steam is condensed to saturated liquid at constant pressure. Calculate the change in the entropy of the universe with this process.
Solution:
Initial state of the steam: superheated at 0.2 MPa and 200oC
H1 = 2870.4 kJ/kg; and s1 = 7.5033 kJ/kgK
Final state: saturated liquid at 0.2 MPa.
H2 = 504.52 kJ/kg and s2 = 1.5295 kJ/kgK
Hence DSsteam = s2 – s1 = 1.5295 – 7.5033 = – 5.9738 kJ/kgK
For a constant pressure process: q = Dh
Therefore, q = h2 – h1 = 504.52 – 2870.4 = – 2365.68 kJ
Entropy change of the surroundings = DSsur = Q/Tsur = 2365.88/300 = 7.886 kJ/K
Hence, DSuni = DSsys + DSsur = -5.9738 +7.886 = 1.9122 kJ/K
DSuni > 0 and hence the process is irreversible and feasible.