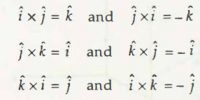Vector or Cross product
If the product of two vectors is a vector quantity, then that product is called vector or cross product. The magnitude of the cross product is obtained by multiplying the magnitudes of their constituent vectors with the sine of the angle between them. The direction of the cross product is determined by the right-handed screw rule.
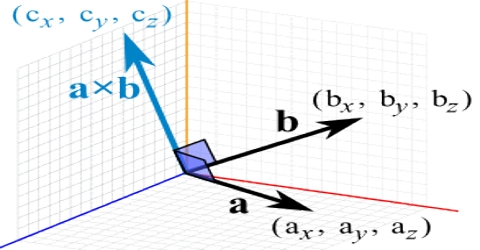
Explanation: Let P→ and Q→ be two vectors acting at O making an angle α. According to the definition, the vector product is,
R→ =P→ × Q→ = η |P| |Q| Sin α = η PQ Sin α
where 0 ≤ α ≤ π
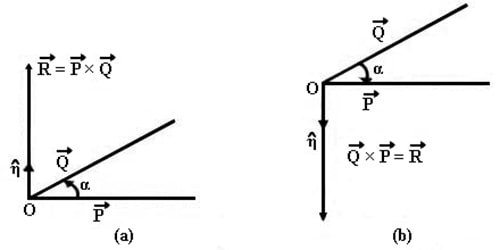
Here η (eta) is a unit vector which represents, the direction of R→ Fig (a) and (b). The direction η is found from the right-handed screw rule.
We can calculate the Cross Product this way: the cross product with angle and unit vector
a × b = |a| |b| sin(θ) η
- |a| is the magnitude (length) of vector a
- |b| is the magnitude (length) of vector b
- θ is the angle between a and b
- η is the unit vector at right angles to both a and b