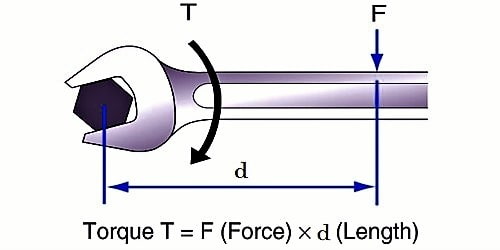
Torque is an appraise of the force that can reason an object to rotate about an axis. It is a vector quantity. The path of the torque vector depends on the direction of the force on the axis. Just as a force is what causes an object to accelerate in linear kinematics, torque is what causes an object to obtain angular acceleration.
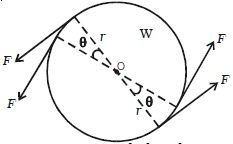
Suppose two equal and opposite forces F act tangentially to a wheel W, and rotate it through an angle θ (Figure).
When a torque does work on a rotating rigid body, the kinetic energy changes by an amount equal to the work done. Work done by a linear force is –
Work = force * distance; in the rotational world, work is done by a torque functional through some angle: work = (torque) * (angle).
Then, the work is done by each force = Force x distance = F x r
(since r θ is the distance moved by a point on the rim)
Total work done W = F r θ +F r θ = 2 Fr θ
but torque τ = F x 2r = 2 F r
so, work done by the couple, W = τθ
The torque is stable, so the angular acceleration is constant. So you can attain it as a function of time.
Work done by a torque can be intended by taking equivalence from work done by force. Work done by the force is calculated as the dot product of force and displacement of the point of the relevance of force. In case of angular motion, force is replaced by torque and linear displacement is replaced by angular displacement. The discussion of work and power makes our treatment of rotational motion approximately comprehensive, with the exception of systematic motion and angular momentum, which are discussed in Angular Momentum.
Examples of the torque or couple are –
- Forces applied to the handle of a screw press,
- Opening or closing a water tap.
- Turning the cap of a pen.
- Steering a car.
Example: A machine must turn around to generate power! A machine with no turning round can deliver torque – like an electric motor – but since no distance is moved by force – no power is formed. As soon as the machine starts to rotate power is created.