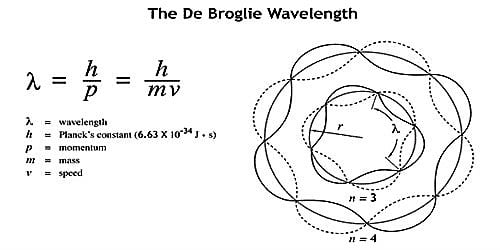
In 1923, Louis de Broglie, a French physicist, projected a proposition to explain the theory of the atomic structure. By using a series of substitution de Broglie hypothesizes particles to hold properties of waves.
The de Broglie wavelength is the wavelength, λ, related to an object and is related to its momentum and mass. The de Broglie equation is an equation used to explain the wave properties of matter, particularly, the wave nature of the electron:
λ = h/mv,
where λ is wavelength, h is Planck’s constant, m is the mass of a particle, moving at a velocity v. de Broglie suggested that particles can demonstrate properties of waves.
Significance of de-Broglie Waves: The wave nature of matter, however, has no significance for objects of ordinary size because the wavelength of the wave associated with them is too small to be detected. This can be illustrated by the following examples.
(i) Suppose we consider an electron of mass 9.1 x 10-31 kg and moving with a velocity of 10-7 ms-1. Its de-Broglie wavelength will be;
λ = h/mv = [(6.626 x 10-34 kgm2s-1) / (9.1 x 10-31 kg * 10-7 ms-1)]
= 0.727 x 10-10 m = 7.27 x 10-11 m
This value of λ can be measured by the method similar to that for the determination of the wavelength of X-rays.
(ii) Let us now consider a ball of mass 10-2 kg moving with a velocity of 102 ms-1. Its de-Broglie wavelength will be;
λ = h/mv = [(6.626 x 10-34 kgm2s-1) / (10-2 kg ×102 ms-1)]
= 6.62 x 10-34 m
This wavelength is too small to be measured, and hence de-Broglie relation has no significance for such a large object. It seemed reasonable to wonder if electrons could also have a dual wave-particle nature.
Objects of everyday understanding, however, have a computed wavelength much lesser than that of electrons, so their wave properties have in no way been detected; recognizable objects show only particle behavior. De Broglie waves play a substantial role, therefore, only in the dominion of subatomic particles. It is only for very tiny objects like electrons that the concept really has much significance.
Thus, de Broglie concept is significant only for sub-microscopic objects in the range of atoms, molecules or smaller sub-atomic particles.
Although de Broglie was credited for his hypothesis, he had no definite investigational confirmation for his assumption. In 1927, Clinton J. Davisson and Lester H. Germer shot electron particles onto a nickel crystal. What they saw was the diffraction of the electron similar to wave’s diffraction against crystals (x-rays). In the same year, an English physicist, George P. Thomson fired electrons towards thin metal foil providing him with similar results as Davisson and Germer.
The wave-like nature of light is having two accommodating investigational proofs as suggested in the De Broglie hypothesis. The experimental proofs are –
- The separate atomic energy levels of the atom in the electronic formation.
- And the diffraction model of electrons from the crystal planes in solid materials. The atomic energy levels, the electron waves can be analyzed as a practical interfering model by using the Bohr model.
- Again, the wave nature of the electrons can be explained, by the particle in box analysis in quantum mechanics.