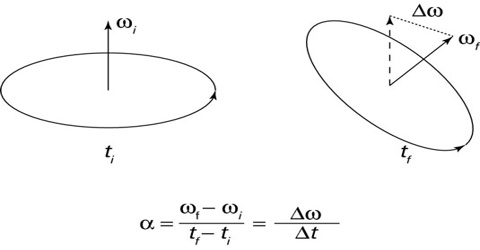
Angular acceleration
Angular acceleration is the rate of change of angular Velocity with respect to time. In many cases angular velocity of a rotating particle increases or decreases. If angular velocity changes then it is understood that the particle is moving with angular acceleration. It is a vector quantity, consisting of a magnitude component and either of two defined directions or senses.
Average angular acceleration of a rotating particle means rate of change of angular velocity for a fixed time interval.
So, if for a very small time interval ∆t the change of angular velocity is ∆ω, then average angular acceleration during that tune interval is,
α = ∆ω/∆t
If time interval tends to zero, thus we get instantaneous angular acceleration.
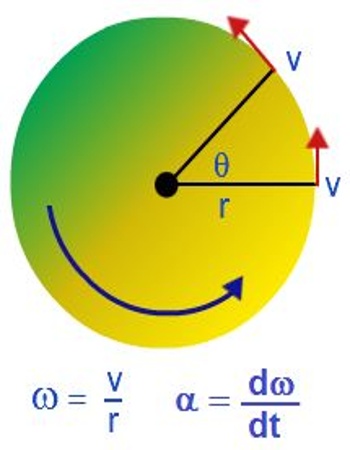
By applying the rule of calculus, we get,
α = lit∆t→0 ∆ω/∆t;
or, α = dω/dt = d/dt (dθ/dt) = d2θ/dt2
Angular acceleration means instantaneous angular acceleration.
Its unit is rad/sec2 (rad s-2)
If the angular acceleration of a rotating particle is constant, then instantaneous angular acceleration is any time Interval is equal to the average angular acceleration. In this case, if rate of change of angular velocity in time t is ω, then angular acceleration, α = ω/t
Dimension of angular acceleration, [α] = [ω/t] = [T-1/T] = [T-2]