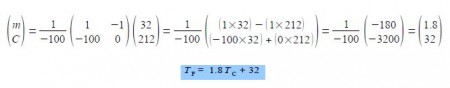There is a linear relationship between the Celsius and Fahrenheit temperature scales such that
TF = mTc + C
Given that the freezing point of pure water is 32°F and 0°C, and the boiling point of pure water 212°F and 100°C, draw up a pair of associated linear equations, transform into matrix form and hence obtain values for the m and C.
Solution
There is a linear relationship between the Celsius and Fahrenheit temperature scales that for two different temperatures which may then be written in matrix form and substituting for the freezing point and normal boiling points of water gives,
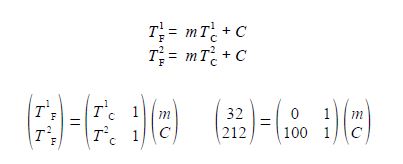
Writing the matrix equation in the standard way for simultaneous equations gives,
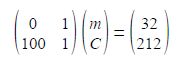
This is in the form A x = b and using the matrix algebra described previously, the determinant ׀A׀, the matrix of cofactors C, the transpose of the matrix of cofactors CT, and the inverse A-1 are, respectively,
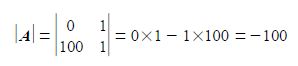
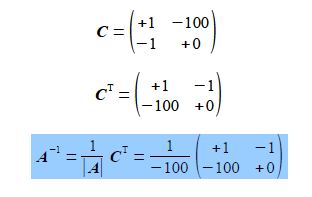
The solution for the unknowns m and C is obtained from x = A-1 b