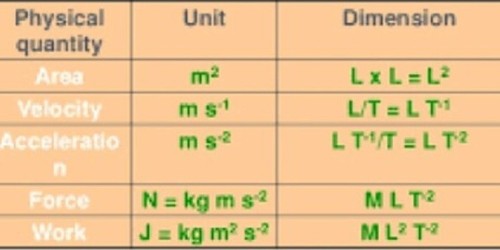
The dimension of a physical quantity is defined as the power to which the fundamental quantities are raised to express the physical quantity. Dimensions of a physical quantity are the powers to which the fundamental quantities must be raised. The dimensional formula is a compound expression showing how and which of the fundamental quantities are involved in making that physical quantity. That is, the dimensional equations are the equations, which represent the dimensions of a physical quantity in terms of the base quantities.
We know that velocity = displacement/time = [L]/[T]
= [M°L1 T-1]
where [M]. [L] and [I] are the dimensions of the fundamental quantities mass, length and time respectively. The dimensional formula is defined as the expression of the physical quantity in terms of its basic unit with proper dimensions. For example, dimensional force is, F = [MLT-2]
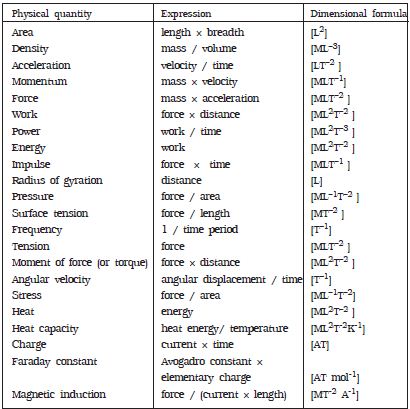
Therefore velocity has zero dimension in mass, one dimension in length and -1 dimension in time. Thus the dimensional formula for velocity is [M0 L1 T-1] or simply [LT-1]. The dimensions of fundamental quantifies are given in Table 1 and the dimensions of some derived quantities are given in Table 2.
Table: dimensions of fundamental quantifies
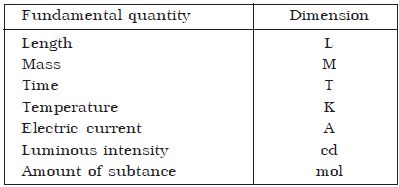
Table: the dimensions of some derived quantities
The dimensional equation is obtained by equating dimensional formula on the right-hand side and left-hand side of an equation. The nature of physical quantity is described by the nature of its dimensions. The dimension of a body means how it is relatable in terms of base quantities. When we define the dimension of a quantity, we generally define its identity and existence. The dimensional equation of a physical quantity is an equation, equating the physical quantity with its dimensional formula.
The dimensional equations have got the following uses:
- To check the accuracy of physical relation.
- To derive the relation between a variety of physical quantities.
- To convert the value of physical quantity from one system of the unit to another system.
- To find the dimension of constants in a given relation.
Rules for writing dimensions of a physical quantity:
Dimensions are always enclosed in [ ] brackets. When the dimensions are simplified we put all the fundamental quantities with their respective power in single [] brackets, for example as in velocity we write [L][T]-1 as [LT-1]. If the dimension is written as it is we take its power to be 1, which is an understood thing.
- Force, [F] = [MLT-2]
- Velocity, [v] = [LT-1]
- Charge, (q) = [AT]
- Specific heat, (s) = [L2T2K-1]
- Gas constant, [R] = [ML2T-2K-1 mol-1]