Half life of a Radioactive Element

The half-life of a Radioactive Element

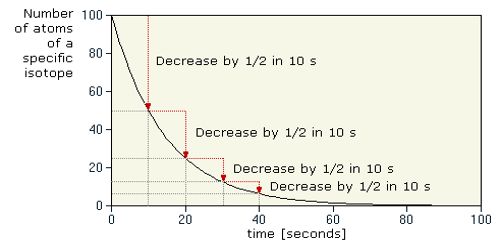
The half-life of a radioactive element is defined as the time during which the number of atoms remaining unchanged becomes half of its initial value. It measures the time it takes for a given amount of the substance to become reduced by half as a consequence of decay, and therefore, the emission of radiation.

From the law of radioactive disintegration we know, N = N₀e^λt

If half life is designated by T, then, when t = T. N = N₀/2

Then, N₀/2 = N₀e^λt

or, e^λt = 2

or, λt = log_e2

then, T = log_e2 / λ = (2.303 x log_e2) / λ

= 0.6933/λ

That means, the half-life of a radioactive element is inversely proportional to the radioactive constant or decay constant of that element.

In order to disintegrate 1 g of uranium to 0.5 g of uranium, it will take 4500 million years. It will take another 4500 million years to disintegrate thus 0.5 g uranium to 0.25 g. So, the half-life of uranium is 4500 million years.

The half-life of isotopes from some sample elements:

• oxygen 16 – infinite
• carbon 14 – 5,730 years
• cobalt 60 – 5.27 years
• silver 94 – .42 seconds

Mathematical Example

What time will it take to decay 60% of a piece of radon? The half-life of radon is 3.82 days.

We know,

Half life, T = 0.6933/λ

or, 3.82 = 0.6933/λ

so, λ = 0.6933/3.82 = 0.1814 day.

If 60% of radon decays, then 40% of it remains i.e., of the 100% an initial number of atoms, 40% remains after decaying 60%.

so, N/N₀ =  40/100.

Here, N₀ = initial number of atoms and

N = rest number of atoms.

We know, N = N₀e^λt

then, N/N₀ = e^λt

or, 40/100 = e^0.1814t or, 2/5 = e^0.1814t

or, ln (2/5) = – 0.1814t

then, t = [ln 2/5] / – 0.1814t = 5.05

Ans. 5.05 days