The Lattice Enthalpy (L.E.)
In an ionic compound, the oppositely charged ions are held together by electrostatic forces of attraction. A quantitative measure of the stability of an ionic solid is given by its lattice energy or lattice enthalpy (L.E.). The lattice enthalpy is defined as the energy released when 1 mole of ionic crystal is formed from its gaseous ions.
For an ionic compound MX the lattice enthalpy is the energy change in the following reaction:
Mn+ (g) + Xn- (g) → MX (s) … … … … (1)
It is an exothermic reaction. If, however, we consider the opposite reaction,
MX (s) → Mn+ (g) + Xn- (g) … … … … (2)
the energy change is termed, the lattice dissociation enthalpy which is defined as the energy required to completely separate one mole of a solid ionic crystal into its gaseous ions.
Lattice dissociation enthalpy (and hence lattice enthalpy) will depend on the attraction between the ions in the ionic crystal. The force of attraction between ions is directly proportional to the product or the charges on the ions and inversely proportional to the square of the distance between the centres of the two ions when they are closest to each other. If Q1 and Q2 are the charges and r is the distance apart then;
The force of attraction ∞ (Q1Q2/r2)
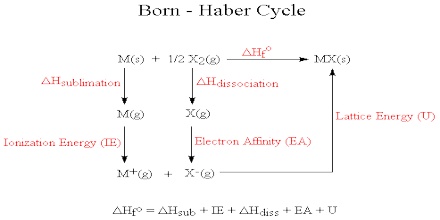
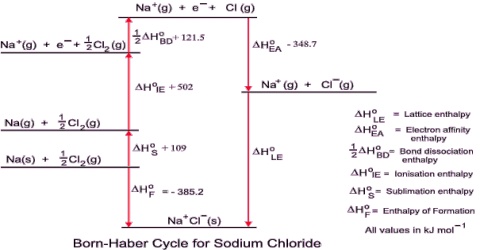
By applying Coulomb’s law it is possible to calculate the lattice enthalpy of simple ionic compounds. Direct experimental measurement of lattice enthalpy is difficult. It is also possible to calculate lattice enthalpies from a thermochemical ‘cycle’ known as Born-Haber Cycle after two German scientists Max Born and Fritz Haber who developed this cycle. The cycle is based on Hess’s law of constant heat summation.
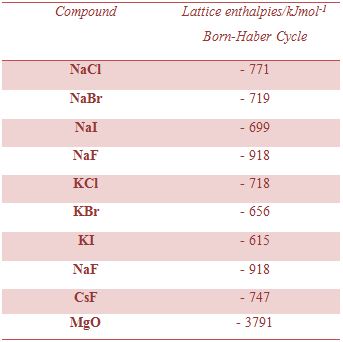
Lattice enthalpies of several ionic Compounds: