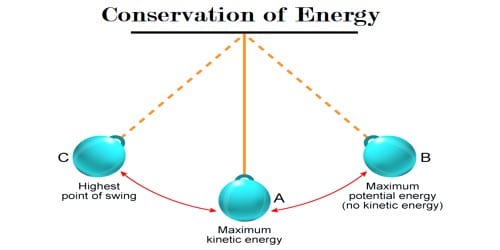
Conservation of Energy in the motion of simple pendulum
In a simple pendulum with no friction, mechanical energy is conserved. When a simple pendulum oscillates with simple harmonic motion, it gains some kinetic energy because of this type of motion. As the pendulum swings back and forth, there is a constant exchange between kinetic energy and gravitational potential energy. The motion of a pendulum is a classic example of mechanical energy conservation. A pendulum consists of a mass (known as a bob) attached by a string to a pivot point. As the pendulum moves, it sweeps out a circular arc, moving back and forth in a periodic fashion. Besides, a restoring force always acts on the bob of the pendulum in the opposite direction of displacement. This gives the mass gravitational potential energy (GPE), which is the energy of position. The work done on the mass is equal to the GPE gained. As a result, work is done during displacement. For this reason, the particle has also some potential energy as well. The force of gravity acts in a downward direction and does work upon the pendulum bob. The other force acting upon the bob is the force of tension. Tension is an external force and if it did do work upon the pendulum bob it would indeed serve to change the total mechanical energy of the bob. If there is no frictional force or similar type of dissipating force acting, the total energy of the simple pendulum will remain constant.
Suppose, a mass of the bob is in and at any moment its displacement and velocity are respectively x and v. So, at that moment kinetic energy of the bob i.e., a simple pendulum is,
Ek = ½ MV2
Since, x = A sin (ωt + δ)
v = dx/dt = d/dt (A sin ωt + δ) = Aω cos (ωt + δ)
Ek = ½ mA2ω2 cos2 (ωt + δ)
Again, ω2 = K/m
So, Ek = ½ mA2 K/m cos2 (ωt + δ)
then, Kinetic energy, KE = ½ KA2 cos2 (ωt + δ) … … … (1)
From equation (1) it is seen that as the maximum value of cos2 (ωt + δ) is 1, hence the maximum kinetic energy is ½ KA2. During motion, the kinetic energy of the particle may change from zero to this maximum value. At all points in the trajectory of the pendulum bob, the angle between the force of tension and its direction of motion is 90 degrees.
Taking δ = 0, the change of kinetic energy has been shown in figures 1 and 2.
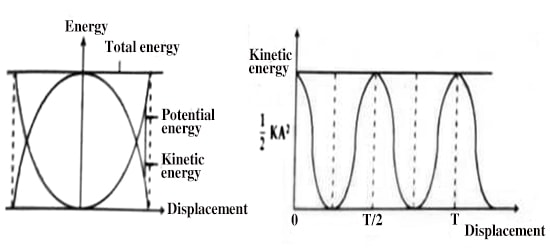
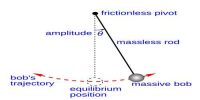
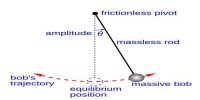
A simple pendulum has a small-diameter bob and a string that has a very little accumulation but is strong enough not to stretch significantly. Also shown are the forces on the bob, which result in a net force of – mg sin θ toward the equilibrium position—that is, a restoring force.