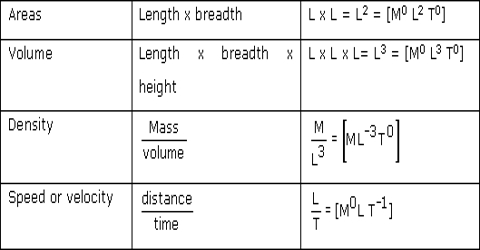
The necessity of Dimensional Equations
The importance of dimensional equation in physics is enormous. Its importance’s are discussed below:
(1) To find the dimension of constants in a given relation. One form of the unit can be converted into another form of unit.
(2) Accuracy of an equation can be verified. Checking the correctness of any equation (i.e, the accuracy of various formulae).
(3) To convert the value of physical quantity from one system of the unit to another system. Equation of different quantifies can be formed.
(4) To change from one system of units to another. Unit of a physical quantity can be determined.
(5) To check the correctness of a physical equation. Solution of a physical problem can be found out. To check the dimensional correctness of a given equation.
(6) To derive the relation between various physical quantities. To find the dimensions and units of a given physical quantity in a given system of units.
(7) To derive the relation between different physical quantities involved in a physical phenomenon. To check the correctness of physical relation.
Limitations of Dimensional Equations
Although dimensional equations have many applications, they have some limitations as well. e.g.
(1) The value of dimensionless constants cannot be determined by this method. We form dimensional equations on the basis of the three Dimensional quantities L, M and T. But, if an unknown quantity is dependent on more than these three quantities, then we cannot form dimensional equations for that unknown quantity. For example, the dimensional equation of thermal conductivity cannot be expressed only by L, M, and T, as it depends on another quantity i.e., on temperature.
(2) Besides, by a dimensional process, we cannot find out the value of dimensionless quantity i.e., of constant. It cannot derive relation or formula if a physical quantity depends upon more than three factors having dimensions. So, Dimensional method cannot be used to derive equations involving addition and subtraction. Therefore, a dimensionally correct equation need not be actually correct. e.g.: a dimension of 1/T and 2π/T are the same.
(3) If a quantity is dependent on trigonometric or exponential functions, this method cannot be used. This method cannot be applied to equations involving exponential and trigonometric functions. It cannot derive a formula containing trigonometric function, exponential function, and logarithmic function. Equations using trigonometric, exponential, and logarithmic functions cannot be deduced. e.g.: y = a cos(ωt − kx) cannot be derived using this method.
(4) It cannot be used if the physical quantity is dependent on more than three unknown variables. It does not test whether a physical quantity is a scalar or a vector. This method cannot be applied to derive formula if in mechanics a physical quantity depends on more than three physical quantities (mass, length, time).
(5) In some cases, it is difficult to guess the factors while deriving the relation connecting two or more physical quantities. It cannot be applied to an equation involving more than three physical quantities. It cannot derive a relation having more than one part in an equation. For example applying this technique s = ut + (1/4) at2 is dimensionally correct whereas the correct relation is s = ut + (1/2) at2.