Let consider a body P moving along the circumference of a circle of radius r with linear velocity v and angular velocity ω as shown in Figure. Let it move from P to Q in time dt and dθ be the angle swept by the radius vector.
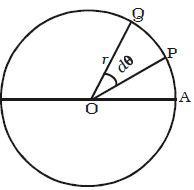
Let PQ = ds, be the arc length covered by the particle moving along the circle, then the angular displacement dθ is expressed as dθ = ds/r. But ds = v dt.
So, dθ = (v dt)/r
Or, dθ/dt = v/r
Angular velocity, ω = v/r, or, v = ω r
In vector notation, v = ω x r
Thus, for a given angular velocity ω, the linear velocity u of the particle is directly proportional to the distance of the particle from the centre of the circular path (i.e) for a body in a uniform circular motion, the angular velocity is the same for all points in the body but linear velocity is different for different points of the body.