Question: Three balloons are filled with different amounts of an ideal gas. One balloon is filled with 3 moles of the ideal gas, filling the balloon to 30 L.
a) One balloon contains 2 moles of gas. What is the volume of the balloon?
b) One balloon encloses a volume of 45 L. How many moles of gas are in the balloon?

Answer:
Avogadro’s law says the volume (V) is directly proportional to the number of molecules of gas (n) at the same temperature.
n ∝ V
This means the ratio of n to V is equal to a constant value.
![]()
Since this constant never changes, the ratio will always be true for different amounts of gas and volumes.
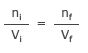
where
ni = initial number of molecules
Vi = initial volume
nf = final number of molecules
Vf = final volume.
Part a) One balloon has 3 moles of gas in 30 L. The other has 2 moles in an unknown volume. Plug these values into the above ratio:
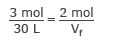
Solve for Vf
(3 mol)Vf = (30 L)(2 mol)
(3 mol)Vf = 60 L⋅mol
Vf = 20 L
You would expect less gas to take up a smaller volume. In this case, 2 moles of gas only took up 20 L.
Part b) This time, the other balloon has a known volume of 45 L and an unknown number of moles. Start with the same ratio as before:
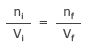
Use the same known values as in part a, but use 45 L for Vf.
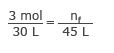
Solve for nf
(3 mol)(45 L) = (30L)nf
135 mol⋅L = (30L)nf
nf = 4.5 moles
The larger volume means there is more gas in the balloon. In this case, there are 4.5 moles of the ideal gas in the larger balloon.
An alternative method would be to use the ratio of the known values. In part a, the known values were the number of moles. There was the second balloon had 2/3 the number of moles so it should have 2/3 of the volume and our final answer is 2/3 the known volume. The same is true of part b. The final volume is 1.5 times larger so it should have 1.5 times as many molecules. 1.5 x 3 = 4.5 which matches our answer. This is a great way to check your work.