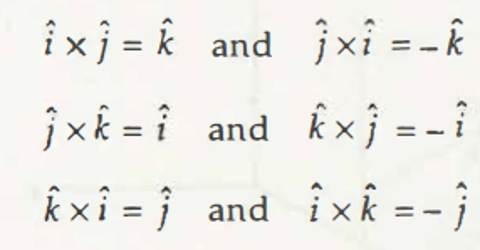Cross Product of Unit Vectors

Cross product of unit vectors

Let î, ĵ and ƙ be the unit vectors along the three co-ordinate axes X, Y and Z respectively which are perpendicular to each other [Figure].

Now, the cross or vector product of

(i) î x î = η |î| |î| Sin 0⁰ [the two unit vectors are acting along the same axis and α = 0]

= η x 1 x 1 x 0 = 0

Similarly, ĵ x ĵ = 0 and ƙ x ƙ = 0

so, î x î = ĵ x ĵ = ƙ x ƙ = 0

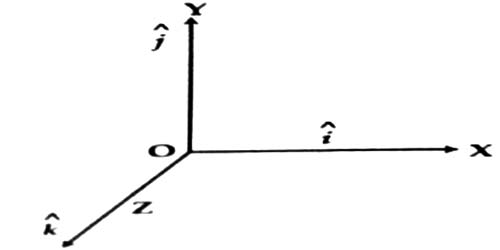
(ii) î x ĵ = η |î| |ĵ| Sin 90⁰ [the two axis are perpendicular to each other and α = 90⁰]

= η x 1 x 1 x 1 = η

Now, according to definition η is normal to both î and ĵ; i.e.,  η is along positive Z-axis.

So, here η and ƙ are identical.

Then, î x ĵ = ƙ

Similarly, ĵ x ƙ = î and ƙ x î = ĵ

so, î x ĵ = ƙ;  ĵ x ƙ = î; ƙ x î = ĵ

Again,

ĵ x î = – (î x ĵ) = – ƙ

ƙ x ĵ = – (ĵ x ƙ) = – î

î x ƙ = – (ƙ x î) = – ĵ

Mathematical Example:

If A^→ = î + ĵ + ƙ and B^→ = 3î + 3ĵ + 3ƙ, show that they are parallel to each other.

We know if A^→ x B^→ = 0, then the vectors A^→ and B^→ are parallel to each other.

Now, A^→ x B^→ = η AB sin α

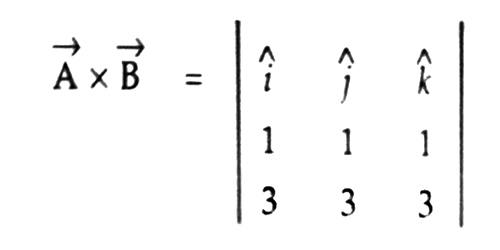
= (3 – 3) î + (3 – 3) ĵ + (3 – 3) ƙ

= 0

so, A^→ x B^→ = η AB sin α = 0

But, A ≠ 0 and B ≠ 0

Hence, Sin α = 0 = Sin 0⁰

so, α = 0

Now we say that, A^→ and B^→ are parallel each other.