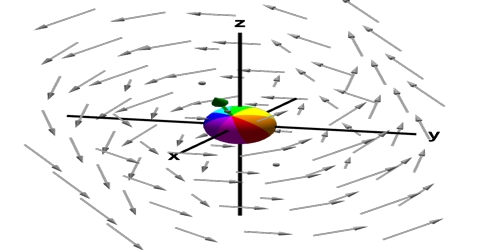
In vector calculus, the curl is a vector operator that describes the insignificant rotation of a 3-dimensional vector field. If the vector field represents the flow velocity of a moving fluid, then the curl is the circulation density of the fluid. The curl measures the degree to which the fluid is rotating about a given point, with whirlpools and tornadoes being extreme examples.
In three dimensional space, if the appropriate vector function of a point is V→ (x, y, z) = (v1 î + v2 ĵ + v3 ƙ), then a vector along the rotational axis is obtained by the cross product of the operator ∆ and V. This type of product is called curl.
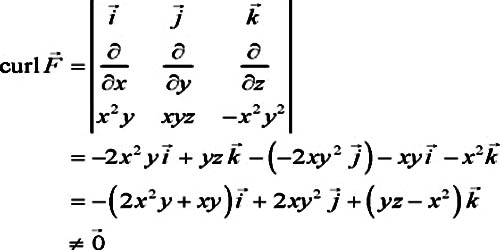
Physical properties of Curl
- If f (x, y, z) has continuous second order partial derivatives then curl (∆f = 0→). This is easy enough to check by plugging into the definition of the derivative.
- If F→ is a conservative vector field then Curl, F→ = 0→. This is a direct result of what it means to be a conservative vector field and the previous fact.
- If F→ is defined on all of Ɍ3 whose components have continuous first-order partial derivative and Curl F→ = 0→ then F→ is a conservative vector field.