Equation for Gravitational Potential Energy near the surface of Earth

Let the mass of the Earth be M and its radius be R. Consider a point A on the surface of the Earth and another point B at a height h above the surface of the Earth. The work done in moving the mass m from A to B is U = U_B – U_A

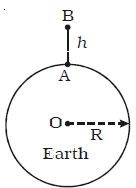
U = – GMm [1/(R+H) – 1/R]

U = GMm [1/R – 1/(R+H)]

So, U = GMmh/R(R+H)

If the body is near the surface of the Earth, h is very small when compared with R. Hence (R+h) could be taken as R.

So, U = GMmh/R²

We know, GM/R² = g,

Then, U = mgh