Experiment: Melde's Experiment

Name of the experiment: Melde’s Experiment

Theory: One end of a thread is fastened to one end of a tuning fork passed the thread through a pulley and a load is attached to the other end of the string in order to make it stretched.

Aim of the experiment: To find out the frequency of an electrically maintained tuning fork by,

(a) Transverse mode of vibration and (b) Longitudinal mode of vibration.

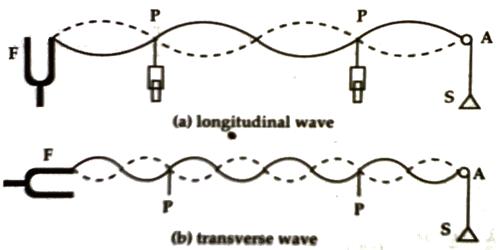
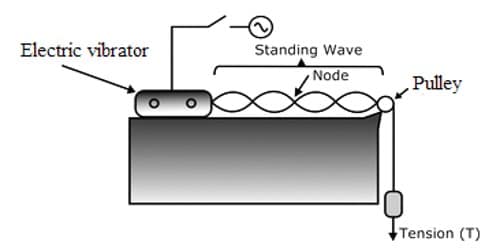
Melde’s experiment set up a light string is tied to one of the prongs of a tuning fork which is mounted on a sounding board. The other end of the string is passed over a horizontal pulley and a light pan is suspended from the free end.

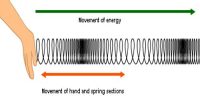
Now, if the tuning fork is vibrated, then two types of the wave will be generated on the thread depending on the direction of vibration. If the direction of vibration of the tuning fork is parallel to the length of the thread. Then longitudinal wave is generated in the thread and frequency of the tuning fork N becomes double the frequency n of the when the direction of vibration of the tuning fork is perpendicular to the length of the thread the transverse wave is produced in the thread and frequency of the tuning fork N, is equal to the frequency ‘n’ of the thread.

In case of transverse wave, N = n = 1/λ √(T/m) … … …. (1)

In case of longitudinal wave, N = 2n = 2/λ √(T/m) … … … (2)

In both cases,

N = frequency of the tuning fork

n = frequency of the thread

λ = wavelength of the wave produced in the thread

T = tension in the thread

m = mass of unit length of the thread.

Instruments: (1) Melde’s instrument, (2) Thread, (3) Metre scale, (4) Weight-box. (5) Clamp.

Procedure:

(1) First of all the tuning fork is placed-in transverse of longitudinal position.

(2) Mass of the Melde’s instrument is taken by a balance.

(3) One end of the experimental thread is fastened to the tuning fork and by taking the other end of the thread through the pulley a load is fastened to the pan.

(4) by placing some weight on the pan the thread is kept stretched.

(5) The tuning fork is struck lightly by a rubber hammer.

(6) by changing the position of the pulley horizontally and by changing weight in the pan the loops and the nodes are made distinct.

(7) Two pin-stands are placed lust below two distinct nodal points and the distance between these two pins is measured by a meter scale. A number of loops are also counted. If the distance between the two pins is, ‘d’ and a number of loops are k, then, λ/2 = d/k. From this, the wavelength can be determined.

(8) Keeping the same weight on the pan and following the same procedure wavelength is measured twice and the mean wavelength is found out.

(9) Now taking weight twice on the pan wavelengths are measured following procedure 1-8 and average λ is found out.

(10) If the tuning fork was kept longitudinally earlier, then now the fork is kept transversely and following the previous procedure average wavelength is determined.

(11) Now the weight and length of the total thread are taken and dividing mass by the length. mass per unit length it is found out.

Then the frequency of the tuning fork for longitudinal and transverse positions is determined by using average wavelength, weight and in of each time.

Calculation and data obtained:

(a) Mass of the scale pan, W = … … g.

(b) Mass of the thread, M = … …. g

(d) Mass per unit length of the thread, m = (M/L) g.

Applications