We assume that a plane wave travels towards a wall with an opening of size D. Behind the wall, we observe wave within a cone of angle θ around the forward direction. At greater angles, the interference leads to cancellation of the wave. This phenomenon is called diffraction: loosely speaking, diffraction is the bending of waves around a corner. Diffraction originates from the interference of outgoing waves originating from the opening. It makes it possible to hear people from room to room, even if we can’t see them [also reflection on walls, floor, and ceiling plays a role].
We use dimensional analysis to find the angle of diffraction θ. The angle is dimensionless [θ] = 1, and depends on the ratio of two length scale & the wavelength λ and the diameter of the opening D. The diffraction phenomenon disappears when either the opening becomes very large or the wavelength becomes very small,
Sin θ = λ/D [rectangular opening].
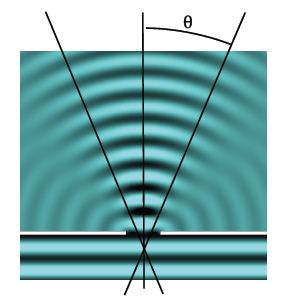
When the opening is a cirde, the above expression must be slightly modified:
sin θ = 1.22 (λ/D) [circular opening].
The factor 1.22 cannot be derived with the tools of undergraduate physics [and mathematics].
Example: A loudspeaker is behind a rectangular opening that is 0.75 m wide. The opening is 18.0 m from a wall, where a person listens to the sound. The loudspeaker produces sounds with different frequencies. Use v = 343 m/s for the speed of sound in air.
a) The loudspeaker produces sound with frequency f = 6.0 kHz. Find the maximum distance from the center, where she can clearly hear the sound.
b) What is the highest frequency that the person can hear when she is standing at a distance x = 2.3 m from the center?
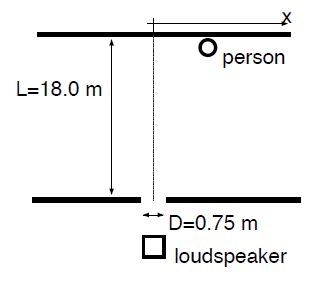
Solution: We have the wavelength of the sound: λ = v/f = (343 m/s)/(6.0 x 103 s-1.) = 0.057 m. The opening has width D = 0.75 m.
This gives the diffraction angle
Sin θ = λ/D = (0.057 m /0.75 m) sin 0 = 0.076, → θ = 4.4°.
Because the person is at a distance L = 18.0 m from the opening, the distance of the person from the center
x = L tan θ = 18.0 m • tan 4.4° = 1.38 m.
We have tan θ = x/L = (2.3 m) / (18.0 m) = 0.128 so that θ = 7.3°. This gives the shortest wavelength:
λ = D sin θ = 0.75 m • sin 7.3° = 0.095 m.
The frequency then follows
f = v/λ = (343 m / 0.095 m) = 3.6 kHz.