Law of reflection
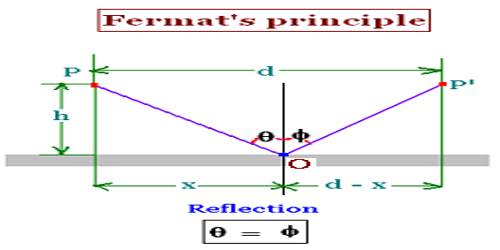
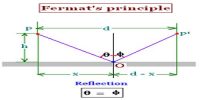
Fermat’s principle states that “light travels between two points along the path that requires the least time, as compared to other nearby paths.” From Fermat’s principle, one can derive the law of reflection [the angle of incidence is equal to the angle of reflection].
Suppose MS is a plane reflector, PO and OQ are incident and reflected rays [Figure]. According to Fermat’s principle, the distance POQ is the shortest distance between P and Q. Now normally PM = h1 and QS = h2 are respectively drawn from Points P and Q on the reflector MS. Let OM = x and MS = l, then OS = (l – x). Here if Initial and final points P and Q are stationary then the distance x between points O and M are only variable.
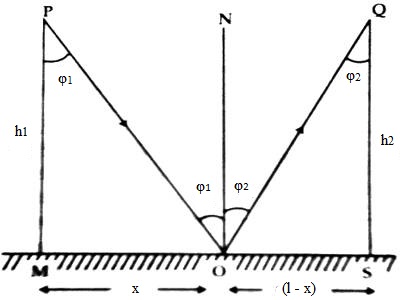
From Figure, POQ = s = PO + OQ
= √(h12 + x2) + √[h22 + (l-x)2]
A light ray incident upon a reflective surface will be reflected at an angle equal to the incident angle. Both angles are typically measured with respect to the normal to the surface. This law of reflection can be derived from Fermat’s principle.
According to Fermat’s principle light ray coming from point P after reflection a point O, the path is along which it reaches to Q will be maximum or minimum. That means,
ds/dx = 0
then, ds/dx = 0 = ½ (h12 + x2)-1/2 2x – ½ [h22 + (l-x)2]-1/2 . 2(l – x)
Or, 0 = x(h12 + x2)-1/2 – (l – x) [h22 + (l-x)2]-1/2
or, x / √(h12 + x2) – (l – x)/√[h22 + (l-x)2] = 0
or, MO/PO – OS/OQ = 0
or, MO/PO = OS/OQ
or, sin OPM = sin OQS, or, sin φ1 = sin φ2
That means, angle of incidence, ∠PON = angle of reflection, ∠OQN.
So, an angle of incidence = angle of reflection.
This is the second law of reflection.
Again, PO and OQ will remain in the normal plane of reflection. Again, ON is the normal on the plane of reflection the plane that PO and OQ form ON remains on that plane. That means, the incident ray PO, reflected ray OQ the normal ON remain on the same place. This is the first law of reflection.
This is the first law of reflection.