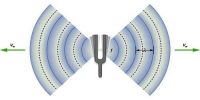
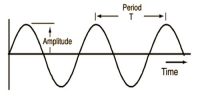
We are familiar with waves on water surfaces such as lakes and oceans. We observe crests and troughs travelling towards the beach at a constant speed v. The motion of crests and trough is called wave propagation. If we take a picture, crests and troughs are observed at equal distances; the distance between troughs [crests] defines the wavelength λ.
If we focus on an object [such as a buoy] on the water surface, the object does not travel towards the shore but rather moves up-and-down with a period T. Because the displacement is perpendicular to the direction of wave propagation, we say that a surface water wave is a transverse wave.
The sound is another familiar example. There is no macroscopic flow of air [wind] associated with sound. Air [and liquids] have no stiffness, and the sound is associated with the periodic condensation and expansion of air in the direction of wave propagation: sound is a longitudinal wave. At a fixed time, regions of compression and expansions are separated by the wavelength λ. On the other hand, at a fixed portion, the air alternatives between condensation and expansion with a period T.
The wave speed v, the wavelength λ, and the period T, of frequency f = 1/T, are related
v= λ/T = f/λ.
Waves propagate energy and momentum; however, no long-range (net) transport of matter is associated with wave phenomena.
Example: The speed of surface waves in shallow waters only depends on the depth d of water: v = √(gd). In water with depth d= 0.65 m, find the period of the oscillatory motion associated with wave motion of wavelength λ = 1.7 m.
Solution: We have the wave speed:
v= √ (9.83 m/s2 * 0.65 m) = 2.5 m/s
For λ = 1.7 m, we find the period T:
T = λ/v = (1.7m / 2.5 m/s) = 0.68s,
or frequency f = 1/(.68 s) = 1.5 Hz.
Discussion: The wave speed decreases as the depth decreases, i.e., as the wave moves towards the shore. Because the frequency remains constant, the wavelength decreases when the wave travels towards the shore. If the equation for the wave speed is used for the deep ocean with d = 4000 m, the wave speed follows v ≈ 200 m/s. This shows that the propagation of disturbances on the ocean is fast [e.g., during a tsunami].
In the above example, the wave speed is independent of the wavelength or the frequency. This is not the case in general, and the wave speed depends on wavelength v = v(λ) or the frequency v = v( f): this dependence is referred to as dispersion.