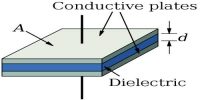
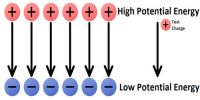
The electric potential energy of two point charges is equal to the work done to assemble the charges or work done in bringing each charge or work done in bringing a charge from the infinite distance.
Let consider a point charge q1, placed at A (Figure].
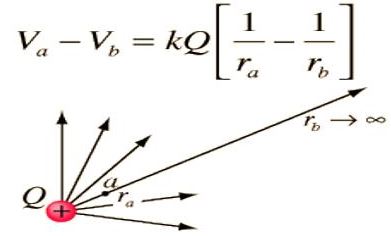
The potential at a point B at a distance r from the charge q1 is
V = q1/(4πε0r)
Another point charge q2 is brought from infinity to the point B.
Now the work done on the charge q2 is stored as electrostatic potential energy (U) in the system of charges q1 and q2.
work is done w = Vq2
Potential Energy: (U) = q1q2/(4πε0r)
Keeping q2 at B, if the charge q1 is imagined to be brought from infinity to the point A, the same amount of work is done.
Also, if both the charges q1 and q2 are brought from infinity, to points A and B respectively, separated by a distance r, the potential energy of the system is the same as the previous cases.
For a system containing more than two charges, the potential energy (U) is given by
U = 1/(4πε0) * [(q1q2/r12) + (q1q3/r13) + (q2q3/r23)]