Preliminary Idea of Differentiation to Describe Motion
Suppose a quantity is dependent on another quantity, then in mathematical language this dependent quantity becomes function of the other quantity. If quantity y is dependent on x, then y is function of x.
i.e., y = f (x)
Again, for exceedingly small change of y, if the small change of x is ∆x, then for the small change of y and x we can write,
y + ∆y = f (∆x + x)
or, ∆y = f (∆x + x) – y
or, ∆y = f (∆x + x) – f(x)
so, ∆x/∆y = [f (∆x + x) – f(x)] / ∆x … … … … (1)
Here, ∆y/∆x is the rate of change of y with respect to x for the above mentioned small change. When the value of ∆x tends to zero, then equation (1) can be written as,
lim∆x→0 = ∆y/∆x = lim∆x→0 [f (∆x + x) – f(x)] / ∆x
Here dy/dx, is the rate of change of y with respect to x for the exceedingly small change of x. dy/dx is called differential co-efficient of y with respect to x and the method of determining the value of dy/dx is called differentiation. For describing motion this differentiation is used.
Here dy/dx is a symbol, which indicates the action of d/dx on y. It is not the division of dy and dx. dy/dx means the rate of variation of y with respect to x.
Suppose you are going with your friend in a motor cycle from “Place A” to “place B”. While going you might notice that the motor cycle was not moving with same speed. Sometimes, it was moving slow, sometimes fast. Sometimes it was stopped by applying brake. So, the motion of the motor cycle was not uniform. But if you are asked to determine the speed of the motor cycle, then by dividing the total distance between “Place A” and “Place B” and time of travel you will find the speed. In this case this speed will mean average speed. That means, change of two positions with respect to time will give speed v, i.e., v = ∆x/∆t.
∆x/∆t is called the rate of change of x with respect to time for the above mentioned change or speed. Again, if the value of time is exceedingly small, then the speed for that time is the instantaneous speed. In this case this speed can be expressed by differentiation, i.e., it ∆t → 0, the fixed value of ∆x/∆t is obtained, then that limiting value lim∆t→0 ∆x/∆t is called rate of change of function x(t) with respect to t or differential co-efficient or instantaneous speed.
Let the path of motion of a particle be AD and at a point B on this path speed is to be determined. Let at time t position of the particle is B and at time t + ∆t the position is C.
In this case, distance between B and C is ∆x and time interval is ∆t. Then the value ∆x of speed, v = ∆x/∆t. In the language of differentiation, this variation of x with respect to t is the magnitude of speed.
Again, for the change ∆t of t, the small ∆y can be expressed graphically [Fig A2). In this case if ∆y that is ∆t is exceedingly small, then ∆y/∆t will indicate the slope of the straight line.
lim∆t→0 ∆y/∆t = slope
or, dy/dt = slope
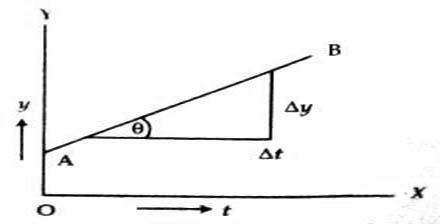
That means, by determining the slope from displacement (y) versus time (t) graph velocity can be determined from the change of displacement with change of time.
Again, let x = f(t) = t2
so, dx/dt = lim∆t→0 ∆x/∆t = lim∆t→0 [f(t + ∆t) – f(t)]
= lim∆t→0 [(t + ∆t)2 – t2]/∆t
= limP→0 [(t + P)2 – t2]/P; (∆t = P suppose)
= limP→0 (2tP + P2)/P = limP→0 (2t + P) = 2t
so, d/dt (t2) = 2t
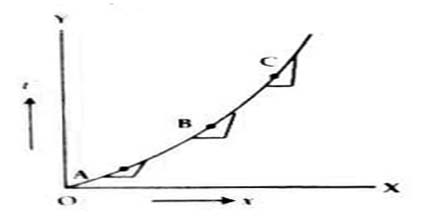
In the graph above, slopes at different points in the curve is not equal. For determining slope at a point in this type of graph an exceedingly small time interval ∆t around ∆x is to be considered. This slope can be shown to be equal to differential co-efficient at that point.
In this case the value of slope = ∆t2/∆x
or, d/dx (t2) = 2t
In figure 3, a graph of t2 versus x has been shown.