The isotherms obtained by plotting the curve PV = nRT are rectangular hyperbolas. Gases approximate to this isotherm at low pressures and high temperatures. The behavior of real gases, however, is better represented by the van der Waals’ equation as pointed out. The accurate measurements of the isotherms of gases have proved exceptionally important in the determination of interatomic forces. When the van der Waals’ equation for one mole is suitably rearranged, we obtain a cubic equation in V as shown below:
V3 – (b + RT/P)V2 + (a/P)V – ab/P = 0 … … … (1)
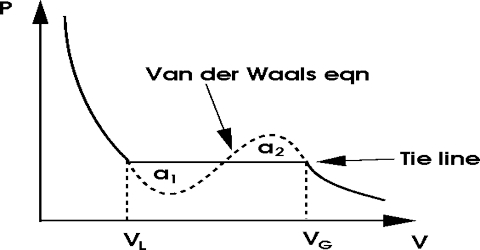
If one plots this equation graphically in the form of a P – V isotherm, a curve of the type ABCFDGE (Figure) is obtained. Such curves may be termed as van der Waals isotherms.
This equation has three roots, i.e., three values of V for any given value of P and T. All three roots may be real or one or two roots real and the others imaginary. When the roots are real and different three different values of V (for a given P and T) are shown in the points B, F and G in curve I. As T increases the three points get closer until they are identical, as in the critical isotherm, curve II. At higher temperatures the curve approximates a rectangular hyperbola, curve III, there bring one real root and two imaginary roots.
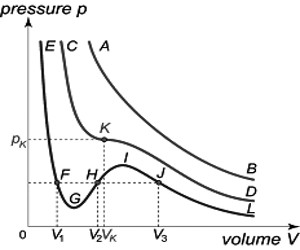
 Fig: Isotherms for CO2 according to van der Waals equation
Fig: Isotherms for CO2 according to van der Waals equation
Andrew’s experiments with carbon dioxide are in agreement with the deduction from the van der Waals equation except for the ≈ shaped portion. Andrews obtained the horizontal portion representing a condensation of the gas, i.e., the equilibrium between gas and liquid. Since three roots of the equation (1) are identical at the critical temperature, there is only one value of V, namely, the critical volume, Vc, which will satisfy this equation when the pressure and temperature have the critical values, Pc and Tc.
It is possible to express the critical constants in terms of the van der Waals constants in the following way:
A cubic equation in V, which has three identical roots, Vc, may be written in the form;
(v – Vc) = 0 … … … (2)
Expanding this equation,
V3 – 3V2. Vc + 3V. Vc2 – Vc3 = 0 … … … (3)
Under the same conditions equations (1) becomes,
V3 – (b + RTc/Pc)V2 + (a/Pc)V – ab/Pc = 0 … … … (4)
Since equations (3) and (4) are simply different ways of writing the same equation, the co-efficient of V3, V2, V, etc. must, therefore, be the same in both the equations. Equating the co-efficient one obtains
3Vc = (b + RTc/Pc); 3Vc2 = (a/Pc); Vc3 = (ab/Pc) … … … (5)
From these equations, one can obtain the following values for Pc, Vc, and Tc.
Vc = 3b; Pc = a/27b2; Tc = 8a/27Rb
If the value of a and b are known, the critical constants may be calculated. Conversely, the equations may be arranged to obtain the expressions;
a = 27/64 (R2Tc2/Pc) and b = RTc/Pc
so that one can calculate a and b from the normal temperature and pressure. The critical volume, Vc has been eliminated from this expression as this is generally less accurately known than the values of Pc and Tc. By combining the equations (5) one may obtain the relation;
RTc/PcVc = 8/3 = 2.67