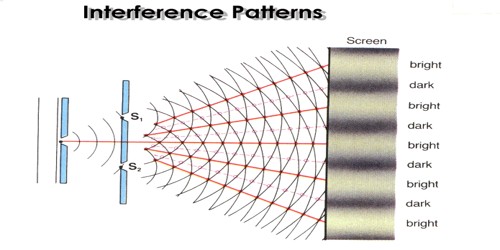
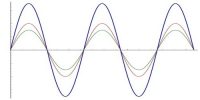
If two light-waves having same frequencies and amplitudes emitted from two coherent sources pass through the same point in a medium, the point becomes very bright when the two waves superpose at that point with the same phase and become dark if the two waves superpose with opposite phase. This phenomenon of variation of intensity of light created due to the superposition of light-waves is called interference.
Let the light from two candles meet at a point. This point will be bright or dark if light waves coming from the candles are respectively of the same phase and opposite phase. Amount of phase difference will depend on the path difference of light and state of phases of the waves. In this case, path difference of light is fixed. But due to the interaction of a particle of candlelight continuously is in a collision with surrounding particles, hence phase changes continuously. As a result, the phrase originated from the vibrations rapidly changes many times. There exist innumerable particles from a candlelight and all probable phases and hence waves emitted from those particles cannot maintain mutual phase relation. So, instead of a permanent interference at a place we see that place equally illuminated.
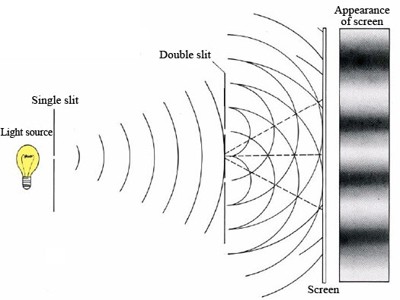
Fig: interference of light
Other Example: If a glass plate is placed on the path of a wave of the two waves that form interference, what change of the fringe will happen?
If a glass plate of thickness t is placed on the way of any one of the two waves, there will be an extra path difference of (μ – 1) t, here, μ = refractive index of glass. As a result, total interference fringes will be shifted towards the glass plate. Although there will be a displacement of interference fringes no change of width of the fringe will occur.