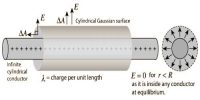
Consider a closed surface S in a non−uniform electric field (Figure).
Consider a very small area “ds” on this surface. The direction of ds is drawn normal to the surface outward. The electric field over ds is supposed to be a constant E→ * E→ and ds→ make an angle θ with each other.
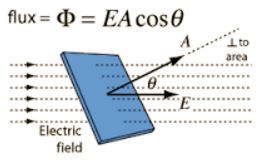
The electric flux is defined as the total number of electric lines of force, crossing through the given area. The electric flux dφ through the area ds is,
dφ = E ds = E ds cosθ
The total flux through the closed surface S is obtained by integrating the above equation over the surface, φ = ϐ dφ = ϐ E. ds
The circle on the integral indicates that the integration is to be taken over the closed surface. The electric flux is a scalar quantity.
Its unit is N m2 C-1.