Indicators in Acid-Base Titrations
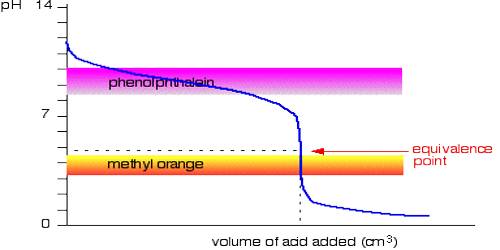
Indicators, as the name implies, are substances which indicate, generally by their color change, the equivalence point, or end point of a titration. There are different types of indicators used in chemical analysis. Here the only acid-base indicators will be dealt with.
Acid-base indicators are usually complex organic compounds which are weak acids or bases. They change their color over a small range of pH. The undissociated form of the indicator has one color and the dissociated form (the anion in the case of an acid indicator and cation in the case of a base indicator) has a different color. As the indicator is used only in very small quantities the color of one form must be quite distinct from that of the other. The color of the solution will depend on the relative proportion of the dissociated and undissociated forms.
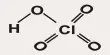
Taking the common indicator phenolphthalein as a weak acid, Hln, its dissociation may be represented by,
Hln (colorless) ↔ ln– (reddish purple) + H+ … …. …. (1)
The equilibrium constant for this equilibrium is given by,
Kln = [H+][ln–] / [Hln] … … … (2)
Kln is the dissociation constant of the indicator and is called the indicator constant.
In an acid solution, the equilibrium will lie to the left as the ionization is repressed (common ion effect) due to the presence of H+ ion in large concentration. The color will be that of Hln. In an alkaline solution, on the other hand, the equilibrium will be shifted towards the right as more Hln will dissociate when the H+ ions are removed by OH+ ions from the alkali. There will be a large concentration of ln– ions and the color will be that of In– . If the acidic and basic forms have two different colors the neutral color is obtained at the pH where the concentration of Hln and In– are equal.
Our eyes are not very sensitive to small color changes. As a result it is often difficult to detect the color change until about 10% of the indicator is neutralized (when it is mostly in the Hln form) and the change does not appear to be complete until about 90 percent of the indicator is neutralized (when it is mostly in the ln– form). Taking logarithm to the base 10 of both sides of equation (16.36) and multiplying both sides of the obtained equation by – 1 one gets,
– log Kln = – log [H+] – log {[ln–] / [Hln]}
Using the definition of pH and pKln
pKln = pH – log {[ln–] / [Hln]} …. … … (3)
Rearrangement of equation 3, gives the relation,
pH = pKln + log {[ln–] / [Hln]}
When the ratio [ln–] / [Hln], is large, say about 90% of the indicator is dissociated,
pH = pKln + log (90/10 or nearly 10)
or, pH = pKln + 1
Again when the ratio [ln–] / [Hln], is small, say about 10% of the indicator is dissociated.
pH = pKln + log (10/90 or nearly 0.1)
or, pH = 1- pKln
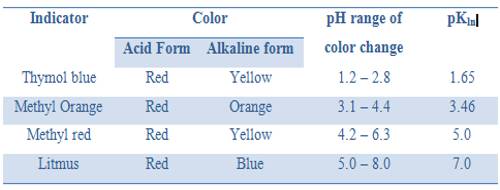
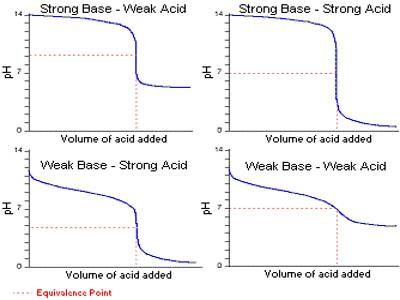
It can be seen from these considerations that our eyes can detect a sharp change of color of the indicator only if during the titration the pH changes over the range pH = pKln ± 1; i.e., over a range of about 1 pH unit on either side of pKln. It is obvious from this discussion that at different indicators indicate neutralization points at different pH values. Table 16.7 gives the pH range of color change for a number of commonly used indicators.
Table: pH range of acid based indicators