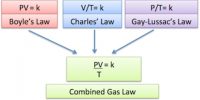
Mathematical Examples of Dalton’s Law:
The total pressure in a gas mixture is the sum of the partial pressures of each individual gas.
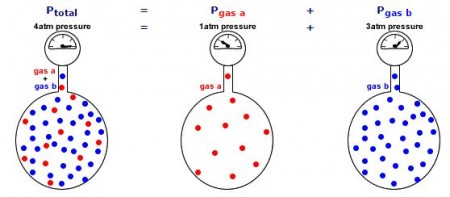
Examples
a) 10 g of nitrogen gas and 10 g of helium gas are placed together in a 10 L container at 25oC. Calculate the partial pressure of each gas and the total pressure of the gas mixture.
Calculate the moles (n) of each gas present: n = mass ÷ molar mass

Calculate the total moles of gas present = 0.4 + 2.5 = 2.9 mol
Calculate the total gas pressure assuming ideal gas behaviour: PV = nRT
P = n x R x T ÷ V
n = 2.9 mol
R = 8.314
T = 25oC = 25 + 273 = 298 K
V = 10 L
P = 2.9 x 8.314 x 298 ÷ 10 = 718 kPa (7atm)
Partial pressure of nitrogen = n(N2) ÷ n(total) x total pressure
Partial pressure of nitrogen = 0.4 ÷ 2.9 x 718 kpa = 99 kPa (0.9 atm)
Partial pressure of helium = n(He) ÷ n(total) x total pressure
Partial pressure of helium = 2.5 ÷ 2.9 x 718 = 619 kPa (6.1atm)
b) At 15oC, 25 mL of neon at 101.3 kPa (1 atm) pressure and 75 mL of helium at 70.9 kPa (0.7 atm) pressure are both expanded into a 1 L sealed flask. Calculate the partial pressure of each gas and the total pressure of the gas mixture.
Since the temperature and moles of each gas is constant, the pressure exerted by each gas is inversely proportional to its volume (Boyle’s Law).
- PiVi = PfVf
- Pf = PiVi ÷ Vf
Partial pressure Neon = 101.3 kPa x 25 x 10-3L ÷ 1 L = 2.5 kPa
Partial pressure Helium = 70.9 kPa x 75 x 10^-3L ÷ 1 L = 5.3 kPa
Total pressure = 2.5 + 5.3 = 7.8 kPa